1) BÀI TOÁN MỞ ĐẦU
Hôm nay tôi lại nhận được 3 bài toán của thầy BìnhKami, 3 bài toán này liên quan đến so sánh 2 lũy thừa cùng cơ số.
- Bài toán 1 : So sánh 2 lũy thừa ${32^{10}}$ và ${16^{15}}$
- Bài toán 2 : So sánh 2 lũy thừa ${2^{100}}$ và ${3^{70}}$
- Bài toán 3 : So sánh 2 lũy thừa ${2^{2017}} – {5^{999}}$
Đối với bài toán số 1 thì tôi đã biết cách làm rồi, cơ số 32 và cơ số 16 đều có thể đưa về cơ số 2, vậy ${32^{10}} = {\left( {{2^5}} \right)^{10}} = {2^{5.10}} = {2^{50}}$ và ${16^{15}} = {\left( {{2^4}} \right)^{15}} = {2^{4.5}} = {2^{60}}$ . Vậy ${32^{10}} < {16^{15}}$ Đối với bài số 2 không thể đưa về cùng cơ số 2 hay 3 vì vậy tôi dùng sự trợ giúp của máy tính Casio, tôi sẽ thiết lập hiệu ${2^{100}} – {3^{70}}$ nếu kết quả ra một giá trị dương thì ${2^{100}} > {3^{70}}$ , thật đơn giản phải không !!
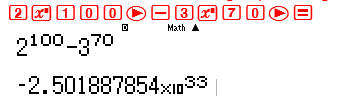
Hay quá ra một giá trị âm, vậy có nghĩa là ${2^{100}} < {3^{70}}$
Tương tự như vậy tôi sẽ làm bài toán số 3 bằng cách nhập hiệu ${2^{2017}} – {5^{999}}$ vào máy tính Casio
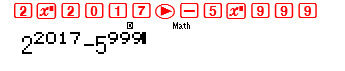
Và tôi bấm nút =
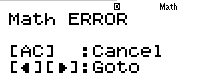
Các bạn thấy đấy, máy tính không tính được. Tôi chịu rồi !!
Để so sánh 2 lũy thừa có giá trị quá lớn mà máy tính Casio không tính được thì chúng ta phải sử dụng một thủ thuật, tôi gọi tắt là BSS. Thủ thuật BSS dựa trên một nguyên tắc so sánh như sau: Nếu số A có n+1 chữ số thì luôn lớn hơn số B có n chữ số .
Ví dụ như số 1000 có 4 chữ số sẽ luôn lớn hơn số 999 có 3 chữ số.
Vậy tôi sẽ xem ${2^{2107}}$ và ${5^{999}}$ thì lũy thừa nào có số chữ số nhiều hơn là xong.
Để làm được việc này tôi sẽ sử dụng máy tính Casio nhưng với tính năng cao cấp hơn, các bạn quan sát nhé:
Đầu tiên là với ${2^{2017}}$
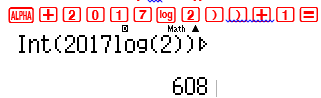
Vậy tôi biết ${2^{2017}}$ có 608 chữ số
Tiếp theo là với ${5^{999}}$

Vậy ${5^{999}}$ có 699 chữ số
Rõ ràng 608> 699 hay ${2^{2017}} < {5^{999}}$ . Thật tuyệt vời phải không !!
Bình luận nguyên tắc hình thành lệnh tính nhanh Casio
Ta thấy quy luật ${10^1}$ có 2 chữ số, ${10^2}$ có 3 chữ số … ${10^k}$ sẽ có k+1 chữ số
Vậy muốn biết 1 lũy thừa A có bao nhiêu chữ số ta sẽ đặt $A = {10^k}$ . Để tìm k ta sẽ logarit cơ số 10 cả 2 vế khi đó k=logA . Vậy số chữ số sẽ là $k + 1 = \left[ {\log A} \right] + 1$
Lệnh Int dùng để lấy phần nguyên của 1 số.
2)VÍ DỤ MINH HỌA
VD1-[Bài toán số nguyên tố Mersenne] Đầu năm 2016, Curtis Cooper và các cộng sự nhóm nghiên cứu Đại học Central Mis-souri, Mỹ vừa công bố số nguyên tố lớn nhất tại thời điểm đó. Số nghuyên tố này là một số có giá trị bằng $M = {2^{74207281}} – 1$ . Hỏi số M có bao nhiêu chữ số.
A. 2233862
B. 22338618
C. 22338617
D. 2233863
GIẢI
Ta có $M = {2^{742007281}} – 1 \Leftrightarrow M + 1 = {2^{742007281}}$
Đặt $M + 1 = {10^k}$ $ \Leftrightarrow {2^{742007281}} = {10^k}$ $ \Leftrightarrow k = \log {2^{74207281}}$ và số chữ số là $\left[ k \right] + 1$
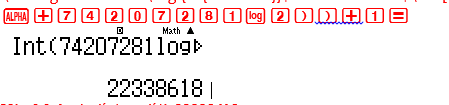
Vậy M+1 có số chữ số là 22338618
Ta nhận thấy M+1 có 22338618 chữ số, vậy M có bao nhiêu chữ số ? Liệu vẫn là 22338618 chữ số hay suy biến còn 22338617 chữ số.
Câu trả lời là không suy biến vì M là lũy thừa bậc của 2 nên tận cùng chỉ có thể là 2, 4, 8, 6 nên khi trừ đi 1 đơn vị vẫn không bị suy biến
Vậy ta chọn B là đáp án chính xác.
Đọc thêm :
$M = {2^{74207281}} – 1$ là số nguyên tố lớn nhất thế giới được phát hiện, gồm 22 triệu chữ số, mất 127 ngày để đọc hết
Giả sử 1 giây bạn có thể đọc được 2 chữ số, bạn không cần ăn uống, ngủ nghỉ…thì 4 tháng liên tục là quãng thời gian mà bạn cần phải bỏ ra để đọc hết con số nguyên tố lớn nhất thế giới do các nhà toán học phát hiện mới đây. Với tên gọi M74207281 con số nguyên tố Merssenne được phát hiện bởi các nhà toán học thuộc GIMPS-tổ chức thành lập năm 1996 chuyên đi tìm những con số nguyên tố.
Câu chuyện đi tìm số nguyên tố bắt đầu từ một nhà toán học, thần học, triết học tự nhiên, Marin Mersenne (1588-1648). Ông là người đã nghiên cứu các số nguyên tố nhằm cố tìm ra một công thức chung đại diện cho các số nguyên tố. Dựa trên các nghiên cứu của ông, các nhà toán học thế hệ sau đã đưa ra một công thức chung cho các số nguyên tố là ${M_p} = {2^p} – 1$ Năm 1750 nhà toán học Ơ-le phát hiện ra số nguyên tố ${M_{31}}$
Năm 1876 số ${M_{127}}$ được nhà toán học Pháp Lucas Edouard phát hiện ra
Năm 1996 số nguyê tố lớn nhất thời đó được phát hiện là ${M_{1398268}}$
VD2-[Khảo sát chất lượng chuyên Lam Sơn – Thanh Hóa năm 2017]
Gọi m là số chữ số cần dùng khi viết số ${2^{30}}$ trong hệ thập phân và n là số chữ số cần dùng khi viết số ${30^2}$ trong hệ nhị phân. Ta có tổng m+n là :
A. 18
B. 20
C. 19
D. 21
GIẢI
Đặt ${2^{30}} = {10^k} \Leftrightarrow k = \log {2^{30}}$ . Số chữ số của ${2^{30}}$ trong hệ thập phân là $\left[ k \right] + 1$

Vậy số chữ số của ${2^{30}}$ trong hệ thập phân là 10
Đặt ${30^2} = 900 = {2^h} \Leftrightarrow h = {\log _2}900$ . Số chữ số của ${30^2}$ trong hệ nhị phân là $\left[ h \right] + 1$
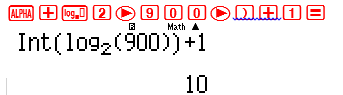
Vậy số chữ số của ${30^2}$ trong hệ nhị phân là 10 $ \Rightarrow m + n = 10 + 10 = 20$
$ \Rightarrow $ Đáp số chính xác là B
VD3: Cho tổng $M = C_{2020}^0 + C_{2020}^1 + C_{2020}^2 + … + C_{2020}^{2020}$ Khi viết M dưới dạng 1 số trong hệ thập phân thì số này có bao nhiêu chữ số:
A. 608
B. 609
C. 610
D. 611
GIẢI
Theo khai triển nhị thức Newtơn thì ${\left( {1 + 1} \right)^{2020}} = C_{2020}^0 + C_{2020}^1 + C_{2020}^2 + … + C_{2020}^{2020}$
Vậy $M = {2^{2020}}$
Đặt ${2^{2020}} = {10^k} \Leftrightarrow k = \log {2^{2020}}$ . Số chữ số của M là $\left[ k \right] + 1$
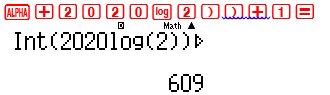
Vậy số chữ số của M là 609. Ta chọn đáp án B
Bình luận
• Bài toán này là sự kết hợp hay giữa kiến thức lũy thừa và kiến thức về nhị thức Newtơn. Để làm được bài toán này bằng Casio thì cần có một số kiến thức cơ bản về tổng Nhị thức Newtơn
• Dạng toán tổng nhị thức Newtơn được tác giả tóm tắt như sau
- Cho khai triển tổng ${\left( {a + b} \right)^n} = C_n^0{a^n}{b^0} + C_n^1{a^{n – 1}}{b^1} + C_n^2{a^{n – 2}}{b^2} + … + C_n^n{a^0}{b^n}$ và khai triển tổng ${\left( {a – b} \right)^n} = C_n^0{a^n}{b^0} – C_n^1{a^{n – 1}}{b^1} + C_n^2{a^{n – 2}}{b^2} – C_n^3{a^{n – 3}}{b^3}… + C_n^n{a^0}{b^n}$
- Để quan sát xem tổng nhị thức Newton có dạng là gì ta quan sát 3 thông số : Thông số mũ n thì quan sát tổ hợp $C_n^1$ ví dụ như xuất hiện $C_{2020}^1$ thì rõ ràng n= 2020 . Thông số a sẽ có số mũ giảm dần, thông số b sẽ có số mũ tăng dần
- Áp dụng $C_{1999}^0{5^{1999}} – C_{1999}^1{5^{1998}}2 + C_{1999}^2{5^{1997}}{2^2} – C_{1999}^3{5^{1996}}{2^3} + …. – C_{1999}^{1999}{2^{1999}}$ thì rõ ràng n=1999 , số mũ của a giảm dần vậy a=5 , số mũ của b tăng dần vậy b=2 . Ta thu gọn khai triển thành ${\left( {5 – 2} \right)^{1999}} = {3^{1999}}$
VD4: So sánh nào sau đây là đúng
A. ${5^{7123}} > {7^{5864}}$
B. ${5^{7123}} < {7^{5864}}$
C. ${3^{400}} < {2^{500}}$
D. ${4^{1700}} > {9^{1200}}$
GIẢI
Đặt ${5^{7123}} = {10^k}$ $ \Leftrightarrow k = \log {5^{7123}} = 7123\log 5 \approx 4978.76 > 4978$
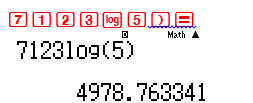
Vậy ${5^{7123}} > {10^{4978}}$
Tương tự đặt ta đặt ${7^{5864}} = {10^h} \Leftrightarrow h = \log {7^{5864}} \approx 4955.65 < 4956$

Vậy ${7^{5864}} < {10^{4956}}$ Tóm lại ${5^{7123}} > {10^{4978}} > {10^{4566}} > {7^{5864}}$
Bình luận :
- Bài toán này nếu ta thực hiện 1 phép Casio ở đẳng cấp thấp là nhập hiệu ${5^{7123}} – {7^{5864}}$ rồi xét dấu thì máy tính không làm được vì vượt qua phạm vi ${10^{100}}$

- Vậy để so sánh ta 2 đại lượng lũy thừa bậc cao M và N ta sẽ đưa về dạng $M > {10^k} > {10^h} > N$
- Tuy nhiên việc so sánh 2 lũy thừa sử dụng Casio ở mức độ đơn giản cũng thường xuất hiện trong đề thi của các trường, vậy ta cũng cần tìm hiểu thêm một chút. Các e xem ở ví dụ số 4 dưới đây.
VD5-[THPT Ngọc Hồi – Hà Nội 2017] Kết quả nào sau đây đúng :
A. ${\left( {\frac{\pi }{6}} \right)^{17}} < {\left( {\frac{\pi }{6}} \right)^{18}}$
B. ${\left( {\frac{\pi }{3}} \right)^{17}} > {\left( {\frac{\pi }{3}} \right)^{18}}$
C. ${\left( {\frac{e}{3}} \right)^{17}} > {\left( {\frac{e}{3}} \right)^{18}}$
D. ${\left( {\frac{e}{2}} \right)^{17}} > {\left( {\frac{e}{2}} \right)^{18}}$
GIẢI
Để kiểm tra tính Đúng – Sai của đáp án A ta sẽ thiết lập hiệu ${\left( {\frac{\pi }{6}} \right)^{17}} – {\left( {\frac{\pi }{6}} \right)^{18}}$. Vậy bài so sánh chuyển về bài bất phương trình ${\left( {\frac{\pi }{6}} \right)^{17}} – {\left( {\frac{\pi }{6}} \right)^{18}} < 0$
Rồi nhập hiệu trên vào máy tính Casio

Rồi ta nhấn nút = nếu kết quả ra 1 giá trị âm thì đáp án A đúng còn ra giá trị dương thì đáp án A sai
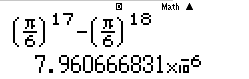
Máy tính Casio báo kết quả ra 1 giá trị dương vậy rõ ràng đáp án A sai.
Tương tự vậy đối với đáp án B

Vậy đáp số B cũng sai
Ta lại tiếp tục với đáp án B

Đây là 1 đại lượng dương vậy ${\left( {\frac{e}{3}} \right)^{17}} – {\left( {\frac{e}{3}} \right)^{18}} > 0$ hay ${\left( {\frac{e}{3}} \right)^{17}} > {\left( {\frac{e}{3}} \right)^{18}}$
Tới đây ta thấy rõ ràng đáp số C là đáp số chính xác !!
Cách 2 : Tự luận
Ta có cơ số $\frac{\pi }{6} \approx 0.52 \in \left( {0;1} \right)$ và số mũ 17<18 vậy ${\left( {\frac{\pi }{6}} \right)^{17}} > {\left( {\frac{\pi }{6}} \right)^{18}}$ $ \Rightarrow $ Đáp án A sai
Ta có cơ số $\frac{\pi }{3} \approx 1.04 > 1$ và số mũ 17<18 vậy ${\left( {\frac{\pi }{3}} \right)^{17}} < {\left( {\frac{\pi }{3}} \right)^{18}}$ $ \Rightarrow $ Đáp án B sai
Ta có cơ số $\frac{e}{3} \approx 0.906 \in \left( {0;1} \right)$ và số mũ 17<18vậy ${\left( {\frac{e}{3}} \right)^{17}} > {\left( {\frac{e}{3}} \right)^{18}}$ $ \Rightarrow $ Đáp số C sai
Bình luận Để so sánh 2 lũy thừa cùng cơ số ${a^u}$ và ${a^v}$ ta sử dụng tính chất sau
- Nếu cơ số a>1 và u>v thì ${a^u} > {a^v}$ (Điều này dẫn tới đáp án B sai)
- Nếu cơ số a thuộc khoảng (0;1) và u>v thì ${a^u} < {a^v}$ (Điều này dẫn tới đáp án A sai)
VD6-[THPT-Hà Nội-Amsterdam 2017] (Bài toán xây dựng để chống lại Casio) Khẳng định nào sau đây sai ?
A. ${2^{\sqrt 2 + 1}} > {2^3}$
B. ${\left( {\sqrt 2 – 1} \right)^{2016}} > {\left( {\sqrt 2 – 1} \right)^{2017}}$
C. ${\left( {1 – \frac{{\sqrt 2 }}{2}} \right)^{2016}} < {\left( {1 – \frac{{\sqrt 2 }}{2}} \right)^{2017}}$
D. ${\left( {\sqrt 3 – 1} \right)^{2017}} > {\left( {\sqrt 3 – 1} \right)^{2016}}$
GIẢI
Để kiểm tra tính Đúng – Sai của đáp án A ta sẽ thiết lập hiệu ${2^{\sqrt 2 + 1}} – {2^3}$. Vậy bài so sánh chuyển về bài bất phương trình ${2^{\sqrt 2 + 1}} – {2^3} > 0$
Rồi nhập hiệu trên vào máy tính Casio
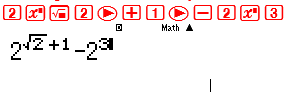
Rồi ta nhấn nút = nếu kết quả ra 1 giá trị dương thì đáp án A đúng còn ra giá trị âm thì đáp án A sai
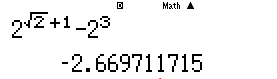
Máy tính Casio báo kết quả ra 1 giá trị âm vậy rõ ràng đáp án A sai.
Tương tự vậy đối với đáp án B

Đáp số máy tính báo là 0 điều này là vô lý vì cơ số khác 0 và số mũ khác nhau buộc ${\left( {\sqrt 2 – 1} \right)^{2016}}$ và ${\left( {\sqrt 2 – 1} \right)^{2017}}$ buộc phải khác nhau.
Như vậy trong trường hợp này thì máy tính chịu !!!
Cách 2: Tự luận
Ngoài phương pháp so sánh 2 lũy thừa cùng cơ số được tác giả trình bày ở Ví dụ 3 thì tại Ví dụ 4 này tác giả xin giới thiệu 1 phương pháp thứ 2 vô cùng hiệu quả có tên là Phương pháp đặt nhân tử chung.
Đáp án B : ${\left( {\sqrt 2 – 1} \right)^{2016}} > {\left( {\sqrt 2 – 1} \right)^{2017}} \Leftrightarrow {\left( {\sqrt 2 – 1} \right)^{2016}} – {\left( {\sqrt 2 – 1} \right)^{2017}} > 0$
$ \Leftrightarrow {\left( {\sqrt 2 – 1} \right)^{2016}}\left[ {1 – \left( {\sqrt 2 – 1} \right)} \right] > 0 \Leftrightarrow \left( {2 – \sqrt 2 } \right){\left( {\sqrt 2 – 1} \right)^{2016}} > 0$
Dễ thấy $2 – \sqrt 2 > 0$ và ${\left( {\sqrt 2 – 1} \right)^{2016}} > 0$ vậy $\left( {2 – \sqrt 2 } \right){\left( {\sqrt 2 – 1} \right)^{2016}} > 0$ Đáp số B đúng
Bình luận Theo thuật toán của Casio thì những đại lượng dương mà nhỏ hơn ${10^{ – 100}}$ hoặc lớn hơn $ – {10^{ – 100}}$ thì sẽ được hiển thị là ố 0 .
Đây là kẽ hở để các trường ra bài toán so sánh lũy thừa chống lại Casio
BÀI TẬP TỰ LUYỆN
Bài 1-[ Bài toán số nguyên tố Fecmat] Nhà toán học Pháp Pierre de Fermat là người đầu tiên đưa ra khái niệm số Fecmat ${F_n} = {2^{{2^n}}} + 1$ là một số nghuyên tố với n là số dương không âm. Hãy tìm số chữ số của ${F_{13}}$
A.1243
B. 1234
C. 2452
D. 2467
*Chú ý : Sự dự đoán của Fecmat là sai lầm vì nhà toán học Ơ le đã chứng minh được ${F_5}$ là hợp số.
Bài 2: Cho tổng $M = C_{1642}^0{3^{1642}} + C_{1642}^1{3^{1641}}2 + C_{1642}^3{3^{1640}}{2^3} + … + C_{1642}^{1642}{2^{1642}}$ Khi viết M dưới dạng 1 số trong hệ thập phân thì số này có bao nhiêu chữ số:
A. 608
B. 609
C. 610
D. 611
*Chú ý : 1642 là năm sinh của nhà toán học, vật lý học, thiên văn học, thần học, giả kim thuật vĩ đại người Anh Isaac Newton.
Bài 3: So sánh nào sau đây là đúng
A. ${11^{2003}} > {9^{2500}}$
B. ${23^{693}} < {25^{600}}$
C. ${29^{445}} < {31^{523}}$ D. ${29^{445}} > {31^{523}}$
Bài 4-[Thi thử THPT Ngọc Hồi – Hà Nội lần 1 năm 2017] Cho a,b là hai số tự nhiên lớn hơn 1 thỏa mãn a+b=10 và ${a^{12}}{b^{2016}}$ là một số tự nhiên có 973 chữ số. Cặp a,b thỏa mãn bài toán là :
A. (5;5)
B. (6;4)
C. (8;2)
D. (7;3)
Bài 5-[THPT Ngọc Hồi – Hà Nội 2017] Kết quả nào sau đây đúng :
A. ${\left( {\frac{\pi }{6}} \right)^{17}} < {\left( {\frac{\pi }{6}} \right)^{18}}$
B. ${\left( {\frac{\pi }{3}} \right)^{17}} > {\left( {\frac{\pi }{3}} \right)^{18}}$
C. ${\left( {\frac{e}{3}} \right)^{17}} > {\left( {\frac{e}{3}} \right)^{18}}$
D. ${\left( {\frac{e}{2}} \right)^{17}} > {\left( {\frac{e}{2}} \right)^{18}}$
Bài 6-[THPT Nguyễn Trãi – Hà Nội 2017] Mệnh đề nào sau đây đúng :
A. ${\left( {\sqrt 3 – \sqrt 2 } \right)^4} < {\left( {\sqrt 3 – \sqrt 2 } \right)^5}$
B. ${\left( {\sqrt {11} – \sqrt 2 } \right)^6} > {\left( {\sqrt {11} – \sqrt 2 } \right)^7}$
C. ${\left( {2 – \sqrt 2 } \right)^3} < {\left( {2 – \sqrt 2 } \right)^4}$
D. ${\left( {4 – \sqrt 2 } \right)^3} < {\left( {4 – \sqrt 2 } \right)^4}$
Bài 7-[THPT Thăng Long – Hà Nội 2017] Khẳng định nào sau đây đúng :
A. ${\left( {{3^2}} \right)^{\frac{1}{2}}} > {\left( {{3^3}} \right)^{\frac{1}{3}}}$
B. ${\left( {2 – \sqrt 3 } \right)^{\sqrt 2 }} > 1$
C. ${\left( {\sqrt 2 – 1} \right)^{ – 3}} > {\left( {\sqrt 2 + 1} \right)^{\sqrt 3 }}$
D. ${\left( {0,3} \right)^{\sqrt 3 }} > {\left( {0,3} \right)^2}$
LỜI GIẢI
Bài 1-[Bài toán số nguyên tố Fecmat] Nhà toán học Pháp Pierre de Fermat là người đầu tiên đưa ra khái niệm số Fecmat ${F_n} = {2^{{2^n}}} + 1$ là một số nghuyên tố với n là số dương không âm. Hãy tìm số chữ số của ${F_{13}}$ trong hệ nhị phân
A.1243
B. 1234
C. 2452
D. 2467
GIẢI
Số ${F_{13}}$ có dạng ${2^{{2^{13}}}} + 1$ . Ta thấy số ${2^{{2^{13}}}} + 1$ không thể tận cùng là 9 nên số chữ số của ${2^{{2^{13}}}} + 1$ cũng chính là số chữ số của ${2^{{2^{13}}}}$ trong hệ thập phân.
Đặt ${2^{{2^{13}}}} = {10^k} \Leftrightarrow k = {2^{13}}\log \left( 2 \right)$ . Số chữ số của ${2^{{2^{13}}}}$ trong hệ thập phân là $\left[ k \right] + 1$
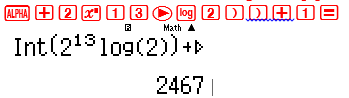
→Đáp số chính xác là D
bài 2: Cho tổng $M = C_{1642}^0{3^{1642}} + C_{1642}^1{3^{1641}}2 + C_{1642}^3{3^{1640}}{2^2} + … + C_{1642}^{1642}{2^{1642}}$ Khi viết M dưới dạng 1 số trong hệ thập phân thì số này có bao nhiêu chữ số:
A. 608
B. 1148
C. 2610
D. 911
*Chú ý : 1642 là năm sinh của nhà toán học, vật lý học, thiên văn học, thần học, giả kim thuật vĩ đại người Anh Isaac Newton.
GIẢI
Rút gọn khai triển nhị thức Newton $M = {\left( {3 + 2} \right)^{1642}} = {5^{1642}}$
Đặt ${5^{1642}} = {10^k} \Leftrightarrow k = 1642\log \left( 5 \right)$ . Số chữ số của ${5^{1642}}$ trong hệ thập phân là $\left[ k \right] + 1$
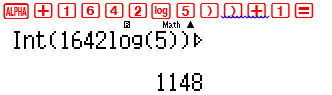
→Đáp số chính xác là B
Bài 3: So sánh nào sau đây là đúng
A. ${11^{2003}} > {9^{2500}}$
B. ${23^{693}} < {25^{600}}$
C. ${29^{445}} < {31^{523}}$
D. ${29^{445}} > {31^{523}}$
GIẢI
Số chữ số của ${11^{2003}}$ và ${9^{2500}}$ trong hệ thập phân lần lượt là:

Số chữ số của ${9^{2500}}$ nhiều hơn số chữ số của ${11^{2003}}$ nên ${9^{2500}} > {11^{2003}}$ $ \Rightarrow $ A sai
Số chữ số của ${23^{693}}$ và ${25^{600}}$ trong hệ thập phân lần lượt là:

Số chữ số của ${23^{693}}$ nhiều hơn số chữ số của ${25^{600}}$ nên ${23^{693}} > {25^{600}}$ $ \Rightarrow $ B sai
Số chữ số của ${29^{445}}$ và ${31^{523}}$ trong hệ thập phân lần lượt là:

Số chữ số của ${29^{445}}$nhỏ hơn số chữ số của ${31^{523}}$ nên ${29^{445}} < {31^{523}}$ $ \Rightarrow $ B là đáp số chính xác
Bài 4: Cho a,b là hai số tự nhiên lớn hơn 1 thỏa mãn a+b=10 và ${a^{12}}{b^{2016}}$ là một số tự nhiên có 973 chữ số. Cặp a,b thỏa mãn bài toán là :
A. (5;5)
B. (6;4)
C. (8;2)
D. (7;3)
GIẢI
Ta có $a + b = 10 \Rightarrow a = 10 – b$ . Khi đó ${a^{12}}{b^{2016}} = {\left( {10 – b} \right)^{12}}{b^{2016}}$
Đặt ${\left( {10 – b} \right)^{12}}{b^{2016}} = {10^k}$ $ \Leftrightarrow k = \log \left[ {{{\left( {10 – b} \right)}^{12}}{b^{2016}}} \right] = 12\log \left( {10 – b} \right) + 2016\log b$
Số chữ số của ${\left( {10 – b} \right)^{12}}{b^{2016}}$ là $\left[ k \right] + 1$
Với đáp số A : a=b=5 . Số chữ số của ${5^{12}}{5^{2016}}$ là 1418 khác 973 $ \Rightarrow $ Đáp số A sai
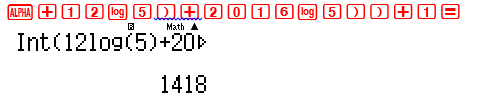
Với đáp số B : a=6, b=4 . Số chữ số của ${6^{12}}{4^{2016}}$ là 1224 khác 973 $ \Rightarrow $ Đáp số B sai
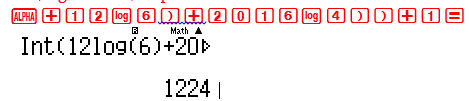
Tương tự với a=7, b=3 . Số chữ số của ${7^{12}}{7^{2016}}$ là 973 $ \Rightarrow $ Đáp số C chính xác