Giải đề thi thử Toán 2018 sở Thanh Hóa bằng máy tính casio
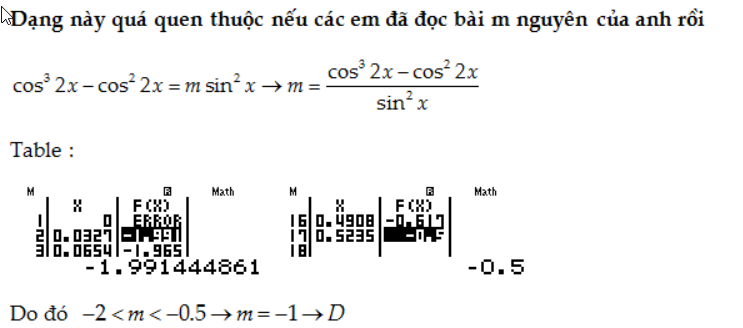
Câu 31. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình cos$^3$(2x)-cos$^2$(2x)=msin$^2$(x) có nghiệm thuộc khoảng (0, π/6)
A.3
B.2
C.0
D.1
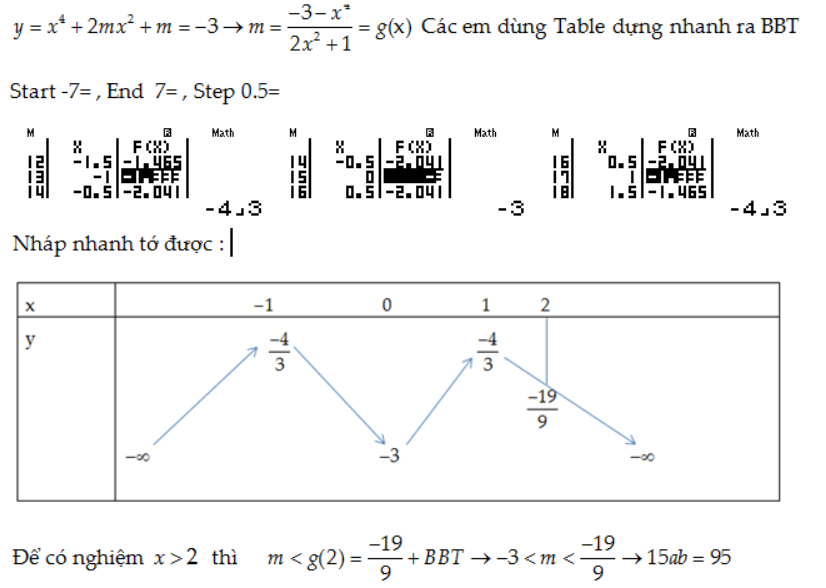
Câu 32: Cho hàm số y=x$^4$+2mx$^2$}+m (m là tham số) . Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số đã cho cắt đường thẳng y=-3 tại bốn điểm phân biệt, trong đó có một điểm có hoành độ lớn hơn 2 còn ba điểm kia có hoành độ nhỏ hơn 1, là khoảng (a;b) (với a,b∈Q , a,b là phân số tối giản). Khi đó 15ab nhận giá trị nào dưới đây?
A. -95
B.95
C. -63
D. 63
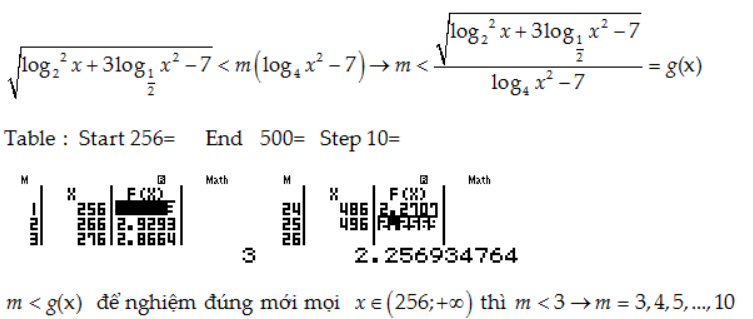
Câu 37: Có bao nhiêu giá trị nguyên của tham số m ∈ [0; 10] để tập nghiệm của bất phương trình $\sqrt {\log _2^2\left( x \right) + 3{{\log }_{\frac{1}{2}}}\left( {{x^2}} \right) – 7} < m\left( {{{\log }_4}\left( {{x^2}} \right) – 7} \right)$ chứa khoảng (256; ∞)
A.7
B.10
C.8
D.9
Câu 41: $f\left( x \right) = {x^3} + b{x^2} + cx + d$ cắt trục hoành tại 3 điểm phân biệt có hoành độ ${x_1};{x_2};{x_3}.$ Tính giá trị biểu thức $P = \frac{1}{{f’\left( {{x_1}} \right)}} + \frac{1}{{f’\left( {{x_2}} \right)}} + \frac{1}{{f’\left( {{x_3}} \right)}}$
A. P = 0
B. $P = \frac{1}{{2b}} + \frac{1}{c}$
C. P = b + c + d D.
P = 3 + 2b + c
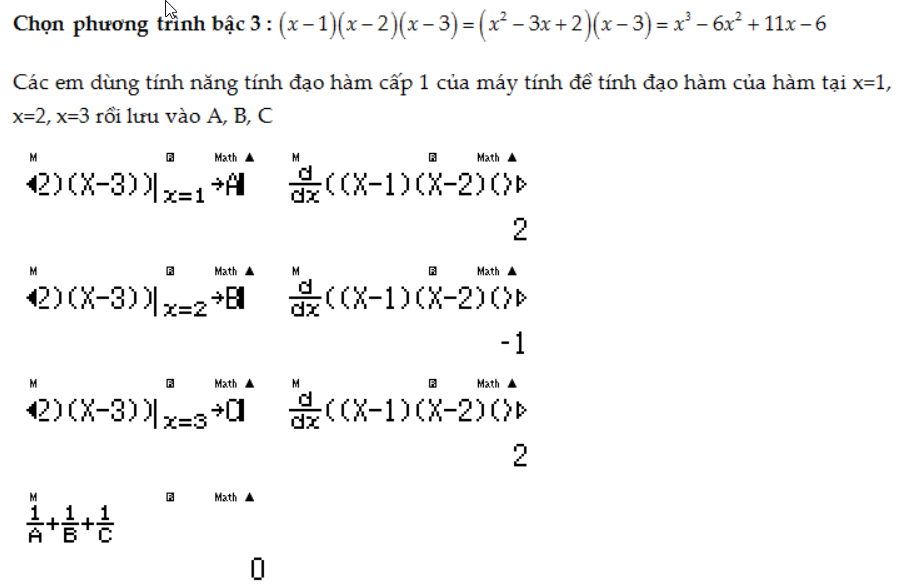
Nguồn: Nguyễn Thế Lực