1) PHƯƠNG PHÁP
Bước 1 : Cô lập m đưa về dạng $m \ge g\left( x \right)$ hoặc $m \le g\left( x \right)$
Bước 2 : Đưa bài toán ban đều về bài toán giải phương trình, bất phương trình đã học.
2) VÍ DỤ MINH HỌA
VD1-[Thi thử chuyên KHTN lần 2 năm 2017]
Tìm tập hợp tất các các giá trị của m để phương trình ${\log _2}x – {\log _2}\left( {x – 2} \right) = m$ có nghiệm :
A. $1 \le m < + \propto $
B. $1 < m < + \propto $
C. $0 \le m < + \propto $
D. $0 < m < + \propto $
GIẢI
Đặt ${\log _2}x – {\log _2}\left( {x – 2} \right) = f\left( x \right)$ khi đó m=f(x) (1). Để phương trình (1) có nghiệm thì m thuộc miền giá trị của f(x) hay $f\left( {\min } \right) \le m \le f\left( {\max } \right)$
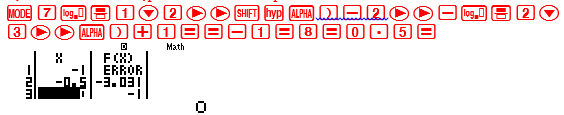
Tới đây bài toán tìm tham số m được quy về bài toán tìm min, max của một hàm số. Ta sử dụng chức năng Mode với miền giá trị của x là Start 2 End 10 Step 0.5

Quan sát bảng giá trị F(X) ta thấy $f\left( {10} \right) \approx 0.3219$ vậy đáp số A và B sai. Đồng thời khi x càng tăng vậy thì F(X) càng giảm. Vậy câu hỏi đặt ra là F(X) có giảm được về 0 hay không.
Ta tư duy nếu F(X) giảm được về 0 có nghĩa là phương trình f(x)=0 có nghiệm. Để kiểm tra dự đoán này ta sử dụng chức năng dò nghiệm SHIFT SOLVE

Máy tính Casio báo phương trình này không có nghiệm. Vậy dấu = không xảy ra
Tóm lại f(x)>0 $ \Leftrightarrow m > 0$ và D là đáp án chính xác
Cách tham khảo : Tự luận
Điều kiện : x>2
Phương trình $ \Leftrightarrow m = {\log _2}\left( {\frac{x}{{x – 2}}} \right)$ $ \Leftrightarrow m = {\log _2}\left( {1 + \frac{2}{{x – 2}}} \right)$
Vì x>2 nên $x – 2 > 0 \Rightarrow 1 + \frac{2}{{x – 2}} > 1$ $ \Rightarrow {\log _2}\left( {1 + \frac{2}{{x – 2}}} \right) > {\log _2}1 = 0$
Vậy $m = \log \left( {1 + \frac{2}{{x – 2}}} \right) > 0$
Bình luận :
- Một bài toán mẫu mực của dạng tìm tham số m ta giải bằng cách kết hợp chức năng lập bảng giá trị MODE 7 và chức năng dò nghiệm SHIFT SOLVE một cách khéo léo.
- Chú ý : m=f(x) mà F(x)>0 vậy m>0 một tính chất bắc cầu hay và thường xuyên gặp
VD2-[Thi thử chuyên KHTN lần 2 năm 2017]
Tìm tham số m để phương trình $\ln x = m{x^4}$ có đúng một nghiệm :
A. $m = \frac{1}{{4e}}$
B. $m = \frac{1}{{4{e^4}}}$
C. $\frac{{{e^4}}}{4}$
D. $\frac{{{e^4}}}{4}$
GIẢI
Cô lập $m = \frac{{\ln x}}{{{x^4}}} = f\left( x \right)$ (m>0)
Tới đây bài toán tìm m trở thành bài toán sự tương giao của 2 đồ thị. Để phương trình ban đầu có đúng 1 nghiệm thì hai đồ thị $y = \frac{{\ln x}}{{{x^4}}}$ và y=m có đúng 1 giao điểm.
Để khảo sát sự biến thiên của hàm $y = \frac{{\ln x}}{{{x^4}}}$ ta sử dụng chức năng MODE với thiết lập Start 0 End 5 Step 0.3

Quan sát sự biến thiên của F(X) ta thấy $f\left( {0.3} \right) \approx – 148.6$ tăng dần tới $F\left( {1.2} \right) \approx 0.0875$ rồi giảm xuống $F\left( 5 \right) \approx 2,{9.10^{ – 3}} \approx 0$
Ta thấy f cực đại $ \approx 0.875$ . Để hai đồ thị $y = \frac{{\ln x}}{{{x^4}}}$ và y=m có đúng 1 giao điểm thì đường thẳng y=m tiếp xúc với đường cong $y = \frac{{\ln x}}{{{x^4}}}$ tại điểm cực đại $ \Rightarrow m \approx 0.875 \approx \frac{1}{{4e}}$
Vậy đáp án A là đáp án chính xác
Cách tham khảo : Tự luận
Điều kiện : x>2
Phương trình $ \Leftrightarrow m = {\log _2}\left( {\frac{x}{{x – 2}}} \right)$ $ \Leftrightarrow m = {\log _2}\left( {1 + \frac{2}{{x – 2}}} \right)$
Vì x>2 nên $x – 2 > 0 \Rightarrow 1 + \frac{2}{{x – 2}} > 1$ $ \Rightarrow {\log _2}\left( {1 + \frac{2}{{x – 2}}} \right) > {\log _2}1 = 0$
Vậy $m = \log \left( {1 + \frac{2}{{x – 2}}} \right) > 0$
Bình luận :
- Một bài toán mẫu mực của dạng tìm tham số m ta giải bằng cách kết hợp chức năng lập bảng giá trị MODE 7 và chức năng dò nghiệm SHIFT SOLVE một cách khéo léo.
- Chú ý : m=f(x) mà f(x)>0 vậy m>0 một tính chất bắc cầu hay và thường xuyên gặp
VD3-[Thi thử THPT Lục Ngạn – Bắc Giang lần 1 năm 2017]
Tìm m để phương trình $4{\left( {{{\log }_2}\sqrt x } \right)^2} – {\log _{\frac{1}{2}}}x + m = 0$ có nghiệm thuộc khoảng (0;1) ?
A. $ – 1 \le m \le \frac{1}{4}$
B. $m < \frac{1}{4}$
C. $0 < m \le \frac{1}{4}$
D. $m \le \frac{1}{4}$
GIẢI
Cô lập $m = – 4{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _{\frac{1}{2}}}x$
Đặt $ – 4{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _{\frac{1}{2}}}x = f\left( x \right)$ khi đó m=f(x) (1). Để phương trình (1) có nghiệm thuộc khoảng (0;1) thì m thuộc miền giá trị của f(x) hay $f\left( {\min } \right) \le m \le f\left( {\max } \right)$khi x chạy trên khoảng (0;1)
Bài toán tìm tham số m lại được quy về bài toán tìm min, max của một hàm số. Ta sử dụng chức năng Mode với miền giá trị của x là Start 0 End 1 Step0.1

Quan sát bảng giá trị F(X) ta thấy $F\left( X \right) \le f\left( {0.7} \right) \approx 0.2497 \approx \frac{1}{4}$ vậy đáp án đúng chỉ có thể là B hoặc D
Tuy nhiên vấn đề là $m = \frac{1}{4}$ có nhận hay không. Nếu nhận thì đáp số D là đúng, nếu không nhận thì đáp số B là đúng.
Để kiểm tra tính chất này ta thế $m = \frac{1}{4}$ vào phương tình $4{\left( {{{\log }_2}\sqrt x } \right)^2} – {\log _{\frac{1}{2}}}x + \frac{1}{4} = 0$ rồi dùng chức năng dò nghiệm SHIFT SOLVE để xem có nghiệm x thuộc khoảng (0;1) không là xong.

Máy tính Casio báo có nghiệm x= 0.7071… thuộc khoảng (0;1) . Vậy dấu = có xảy ra
Tóm lại $m \le \frac{1}{4}$ và D là đáp án chính xác
Cách tham khảo : Tự luận
Điều kiện : x>0
Ta có $m = – 4{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _{\frac{1}{2}}}x = – 4{\left( {\frac{1}{2}{{\log }_2}x} \right)^2} – {\log _2}x = – {\left( {{{\log }_2}x} \right)^2} – {\log _2}x$
Vây $m = \frac{1}{4} – {\left( {{{\log }_2}x + \frac{1}{2}} \right)^2} \le \frac{1}{4}$
Dấu = xảy ra $ \Leftrightarrow {\log _2}x + \frac{1}{2} = 0 \Leftrightarrow {\log _2}x = – \frac{1}{2} \Leftrightarrow x = {2^{ – \frac{1}{2}}} = \frac{1}{{\sqrt 2 }}$
Bình luận : Để xem dấu = xảy ra hay không thì ta sẽ thử cho dấu = xảy ra và sử dụng chức năng dò nghiệm. Nếu xuất hiện nghiệm thỏa mãn yêu cầu đề bài thì dấu = xảy ra.
VD4-[Thi HK1 chuyên Amsterdam -HN năm 2017]
Với giá trị nào của tham số m thì phương trình ${\log _{\frac{1}{2}}}\left| {x – 2} \right| – {\log _{\frac{2}{3}}}\left( {x + 1} \right) = m$ có 3 nghiệm phân biệt ?
A. m>3
B. m<2
C. m>0
D. m=2
GIẢI
Đặt ${\log _{\frac{1}{2}}}\left| {x – 2} \right| – {\log _{\frac{2}{3}}}\left( {x + 1} \right) = f\left( x \right)$ khi đó m=f(x) (1).
Bài toán tìm tham số m trở lại bài toán sự tương giao của 2 đồ thị. Để phương trình ban đầu có 3 nghiệm thì đường thẳng y=m cắt đồ thị hàm số y=f(x) tại 3 điểm phân biệt
Ta có y=m là đường thẳng song song với trục hoành
Để khảo sát sự biến thiên của đồ thị hàm số y=f(x) ta sử dụng chức năng lập bảng giá trị TABLE với thiết lập Start -1 End 8 Step 0.5
Quan sát bảng giá trị ta mô tả được sự biến thiên của hàm $f\left( x \right)$ như sau
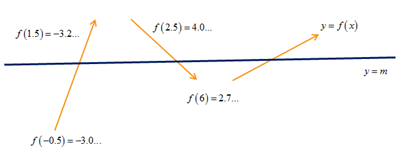
Rõ ràng m<2 thì 2 đồ thị trên cắt nhau tại 1 điểm $ \Rightarrow $ Đáp số B sai
M=2 cũng cắt nhau tai 1 điểm $ \Rightarrow $ Đáp án C và D cùng sai
Vậy đáp số chính xác là A
Bình luận: Bài toán thể hiện được sức mạnh của máy tính Casio đặc biệt trong việc khảo sát các hàm chứa dấu giá trị tuyệt đối. Cách tự luận rất rắc rối vì phải chia làm nhiều khoảng để khảo sát sự biến thiên nên tác giả không đề cập.
VD5-[Thi HK1 THPT Chu Văn An -HN năm 2017]
Tìm tất cả các giá trị thực của tham số m để phương trình ${9^x} – {3^{x + 2}} + m = 0$ có hai nghiệm trái dấu
A. m<0
B. 0<m<8
C. $m \in \left( {0;\frac{{81}}{4}} \right)$
D. Không tồn tại m
GIẢI
Cô lập $m = – {9^x} + {3^{x + 2}}$
Đặt $ – {9^x} + {3^{x + 2}} = f\left( x \right)$ khi đó m=f(x) (1) . Bài toán quy về dạng tương giao của 2 đồ thị.
Để khảo sát sự biến thiên của hàm số y=f(x) và đường đi của đồ thị ta sử dụng chức năng lập bảng giá trị MODE 7 với thiết lập Start -9 End 10 Step 1.

Quan sát bảng giá trị ta mô tả đường đi của đồ thị hàm y= f(x) như sau:
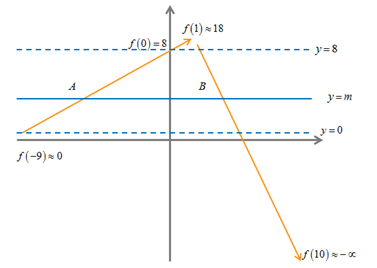
Nhìn sơ đồ ta thấy để đường thẳng y=m cắt đồ thị y=f(x) tại 2 điểm A và B có hoành độ trái dấu thì 0<m<8 => C là đáp án chính xác
Cách tham khảo : Tự luận
Đặt ${3^x} = t\,\,\left( {t > 0} \right)$ . Phương trình $ \Leftrightarrow f\left( t \right) = {t^2} – 9t + m = 0$ (1)
Khi x>0 thì $t > {3^0} = 1$ . Khi x<0 thì t<1 . Vậy để phương trình ban đầu có 2 nghiệm trái dấu thì phương trình (1) có 2 nghiệm dương thỏa mãn ${t_1} < 1 < {t_2}$ Vây $ \Leftrightarrow \left\{ \begin{array}{l} \Delta > 0\\ S > 0\\ P > 0\\ af\left( 1 \right) < 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 81 – 4m > 0\\ 9 > 0\\ m > 0\\ 1.\left( {m – 8} \right) < 0 \end{array} \right. \Leftrightarrow 0 < m < 8$
Dấu = xảy ra $ \Leftrightarrow {\log _2}x + \frac{1}{2} = 0 \Leftrightarrow {\log _2}x = – \frac{1}{2} \Leftrightarrow x = {2^{ – \frac{1}{2}}} = \frac{1}{{\sqrt 2 }}$ Bình luận : • Hai giao điểm có hoành độ trái dấu thì phải nằm về 2 phía của trục tung • Đáp án A sai vì 2 đồ thị chỉ cắt nhau tại 1 điểm nằm ở bên phải trục tung • Nếu 18>m>8 thì 2 đồ thị cắt nhau tại 2 điểm đều nằm bên phải trục tung vậy đáp án C sai.
BÀI TẬP TỰ LUYỆN
Bài 1-[Thi HSG tỉnh Ninh Bình năm 2017]
Tìm tất cả các giá trị thực của tham số mđể phương trình ${4^{{x^2}}} – {2^{{x^2} + 2}} + 6 = m$ có 3 nghiệm phân biệt ?
A. m=3
B. m>2
C. $2 \le m \le 3$
D. $2 < m < 3$
Bài 2-[Thi thử THPT Lục Ngạn – Bắc Giang lần 1 năm 2017] Số nguyên dương lớn nhất để phương trình ${25^{1 + \sqrt {1 – {x^2}} }} – \left( {m + 2} \right){5^{1 + \sqrt {1 – {x^2}} }} + 2m + 1 = 0$ có nghiệm ? A. 20 B. 35 C. 30 D. 25 Bài 3-[Thi HK1 chuyên Amsterdam -HN năm 2017] Tập giá trị của tham số m để phương trình ${5.16^x} – {2.81^x} = m{.36^x}$ có đúng 1 nghiệm ?
A. m>0
B. $\left[ \begin{array}{l} m \le – \sqrt 2 \\ m \ge \sqrt 2 \end{array} \right.$
C. Với mọi m
D. Không tồn tại m
Bài 4-[Thi HK1 THPT Ngô Thì Nhậm – HN năm 2017]
Phương trình ${\log _3}x – {\log _3}\left( {x – 2} \right) = {\log _{\sqrt 3 }}m$ vô nghiệm khi :
A. m>1
B. m<0
C. $0 < m \le 1$ D. $m \le 1$ LỜI GIẢI BÀI TẬP TỰ LUYỆN Bài 1-[Thi HSG tỉnh Ninh Bình năm 2017] Tìm tất cả các giá trị thực của tham số mđể phương trình ${4^{{x^2}}} – {2^{{x^2} + 2}} + 6 = m$ có 3 nghiệm phân biệt ? A. m=3 B. m>2
C. $2 \le m \le 3$
D. 2<m<3
GIẢI
Đặt $f\left( x \right) = {4^{{x^2}}} – {2^{{x^2} + 2}} + 6$. Khi đó phương trình ban đầu $ \Leftrightarrow f\left( x \right) = m$
Sử dụng Casio khảo sát sự biến thiên của đồ thị hàm số y=f(x) với thiết lập Start -4 End 5 Step 0.5

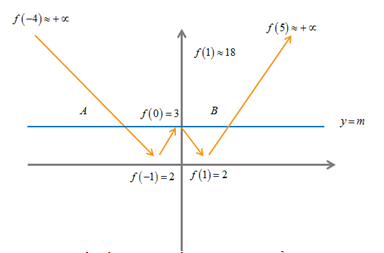
Quan sát bảng biến thiên ta vẽ đường đi của hàm số
Rõ ràng y=3 cắt đồ thị hàm số y=f(x) tại 3 điểm phân biệt vậy đáp án A là chính xác
Cách tham khảo: Tự luận
Đặt ${2^{{x^2}}} = t$ khi đó phương trình ban đầu $ \Leftrightarrow {t^2} – 4t + 6 – m = 0$ (1)
Ta để ý tính chất sau : Nếu t=1 thì x=0 còn nếu $t > 0;t \ne 1$ thì $x = \pm \sqrt {{{\log }_2}t} $ . Vậy để phương trình ban đầu có 3 nghiệm phân biệt thì (1) có 2 nghiệm trong đó có 1 nghiệm t=0 và 1 nghiệm t>0
Với $t = 1 \Rightarrow f\left( 1 \right) = 0 \Rightarrow 3 – m = 0 \Leftrightarrow m = 3$
Bài 2-[Thi thử THPT Lục Ngạn – Bắc Giang lần 1 năm 2017]
Số nguyên dương lớn nhất để phương trình ${25^{1 + \sqrt {1 – {x^2}} }} – \left( {m + 2} \right){5^{1 + \sqrt {1 – {x^2}} }} + 2m + 1 = 0$ có nghiệm ?
A. 20
B. 35
C. 30
D. 25
GIẢI
Cô lập m ta được $m = \frac{{{{25}^{1 + \sqrt {1 – {x^2}} }} – {{2.5}^{1 + \sqrt {1 – {x^2}} }} + 1}}{{{5^{1 + \sqrt {1 – {x^2}} }} – 2}}$
Đặt $f\left( x \right) = \frac{{{{25}^{1 + \sqrt {1 – {x^2}} }} – {{2.5}^{1 + \sqrt {1 – {x^2}} }} + 1}}{{{5^{1 + \sqrt {1 – {x^2}} }} – 2}}$. Khi đó phương trình ban đầu $ \Leftrightarrow f\left( x \right) = m$
Sử dụng Casio khảo sát sự biến thiên của đồ thị hàm số $y = f\left( x \right)$ với thiết lập Start -1 End 1 Step 2

Quan sát bảng biến thiên ta thấy $f\left( x \right) \le f\left( 0 \right) = 25.043…$ hay $m \le f\left( 0 \right)$ vậy m nguyên dương lớn nhất là 25 $ \Rightarrow $ D là đáp án chính xác
Cách tham khảo: Tự luận
Điều kiện $1 – {x^2} \ge 0 \Leftrightarrow – 1 \le x \le 1$ . Ta có $1 – {x^2} \le 1 \Leftrightarrow 1 + \sqrt {1 – {x^2}} \le 2$
Đặt ${5^{1 + \sqrt {1 – {x^2}} }} = t \Rightarrow {5^1} \le t \le {5^2} \Leftrightarrow 5 \le t \le 25$
Phương trình ban đầu trở thành ${t^2} – \left( {m + 2} \right)t + 2m + 1 = 0$ $ \Leftrightarrow m = \frac{{{t^2} – 2t + 1}}{{t – 2}} = f\left( t \right)$
Vậy $m \le f\left( {\max } \right)$
Khảo sát sự biến thiên của hàm f(x) trên miền (5;25) ta được f(max)= f(25)= 25.043
Vậy m nguyên dương lớn nhất là 25
Bài 3-[Thi HK1 chuyên Amsterdam -HN năm 2017]
Tập giá trị của tham số m để phương trình ${5.16^x} – {2.81^x} = m{.36^x}$ có đúng 1 nghiệm ?
A. m>0
B. $\left[ \begin{array}{l} m \le – \sqrt 2 \\ m \ge \sqrt 2 \end{array} \right.$
C. Với mọi m
D. Không tồn tại m
GIẢI
Cô lập m ta được $m = \frac{{{{5.16}^x} – {{2.81}^x}}}{{{{36}^x}}}$
Đặt $f\left( x \right) = \frac{{{{5.16}^x} – {{2.81}^x}}}{{{{36}^x}}}$. Khi đó phương trình ban đầu $ \Leftrightarrow f\left( x \right) = m$
Sử dụng Casio khảo sát sự biến thiên của đồ thị hàm số y=f (x) với thiết lập Start -9 End 10 Step 1
Quan sát bảng biến thiên ta thấy f(x) luôn giảm hay hàm số y=f(x) luôn nghịch biến.
Điều này có nghĩa là đường thẳng y=m luôn cắt đồ thị hàm số y=f(x) tại 1 điểm $ \Rightarrow $ C chính xác
Cách tham khảo: Tự luận
Phương trình ban đầu $ \Leftrightarrow {5.16^x} – m{.36^x} – {2.81^x} = 0$ (1)
Chia cả 2 vế của (1) cho ${81^x}$ ta được: $5.{\left( {\frac{{16}}{{81}}} \right)^x} – m.{\left( {\frac{{36}}{{81}}} \right)^x} – 2 = 0 \Leftrightarrow 5{\left( {\frac{4}{9}} \right)^{2x}} – m{\left( {\frac{4}{9}} \right)^x} – 2 = 0$ (2)
Đặt ${\left( {\frac{4}{9}} \right)^x} = t\,\,\,\,\left( {t > 0} \right)$ (2) $ \Leftrightarrow 5{t^2} – mt – 2 = 0$ (3)
Phương trình (3) có 5.(-2)= -10<0 tức là (3) luôn có 2 nghiệm trái dấu $ \Rightarrow $ (3) luôn có 1 nghiệm dương 1 nghiệm âm $ \Rightarrow $ Phương trình ban đầu luôn có 1 nghiệm với mọi m
Bài 4-[Thi HK1 THPT Ngô Thì Nhậm – HN năm 2017] Phương trình ${\log _3}x – {\log _3}\left( {x – 2} \right) = {\log _{\sqrt 3 }}m$ vô nghiệm khi :
A. m>1
B. m<0
C. $0 < m \le 1$ D. $m \le 1$
GIẢI
Điều kiện : x>2. Phương trình ban đầu $ \Leftrightarrow {\log _3}\left( {\frac{x}{{x – 2}}} \right) = 2{\log _3}m \Leftrightarrow \frac{1}{2}{\log _3}\left( {\frac{x}{{x – 2}}} \right) = {\log _3}m$
$ \Leftrightarrow lo{g_3}\sqrt {\frac{x}{{x – 2}}} = {\log _3}m \Leftrightarrow m = \sqrt {\frac{x}{{x – 2}}} $
Để phương trình ban đầu vô nghiệm thì đường thẳng y=m không cắt đồ thị hàm số $y = f\left( x \right) = \sqrt {\frac{x}{{x – 2}}} $
Sử dụng Casio khảo sát sự biến thiên của đồ thị hàm số y=f(x) với thiết lập Start 2 End 10 Step 0.5

Để khảo sát chính xác hơn ta tính giới hạn của hàm f(x) khi x tiến tới 2 cận là 2 và $ + \propto $

Vậy $\mathop {\lim }\limits_{x \to + \propto } = 1$

Vậy $\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = + \propto $
Quan sát bảng giá trị và 2 giới hạn ta vẽ đường đi cả đồ thị hàm số $y = f(x)$ và sự tương giao
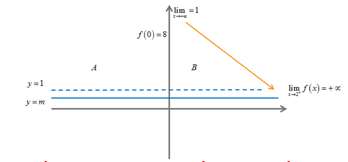
Ta thấy ngay $m \le 1$ thì 2 đồ thị không cắt nhau hay phương trình ban đầu vô nghiệm


