1) PHƯƠNG PHÁP 3: LẬP BẢNG GIÁ TRỊ MODE 7
Bước 1: Chuyển bài toán bất phương trình về bài toán xét dấu bằng cách chuyển hết các số hạng về vế trái. Khi đó bất phương trình sẽ có dạng Vế trái $ \ge 0$ hoặc Vế trái $ \le 0$
Bước 2: Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính Casio để xét dấu các khoảng nghiệm từ đó rút ra đáp số đúng nhất của bài toán .
*Chú ý: Cần làm nhiều bài toán tự luyện để từ đó rút ra kinh nghiệm thiết lập Start End Step hợp lý
Ví dụ minh họa
VD1-[Chuyên Khoa học tự nhiên 2017 ] Bất phương trình ${\log _{\frac{1}{2}}}\left( {{{\log }_3}\frac{{2x + 1}}{{x – 1}}} \right) > 0$ có tập nghiệm là :
A. $\left( { – \propto ; – 2} \right)$
B. $\left( {4; + \propto } \right)$
C. $\left( { – 2;1} \right) \cup \left( {1;4} \right)$
D. $\left( { – \propto ; – 2} \right) \cup \left( {4; + \propto } \right)$
GIẢI
Đăng nhập MODE 7 và nhập vế trái vào máy tính Casio

Quan sát các cận của đáp số là -2;4;1 nên ta phải thiết lập miền giá trị của X sao cho X chạy qua các giá trị này . Ta thiết lập Start -4 End 5 Step 0.5
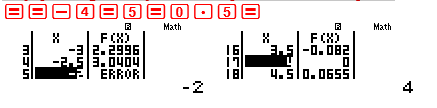
Quan sát bảng giá trị ta thấy rõ ràng hai khoảng $\left( { – \propto ; – 2} \right)$ và $\left( {4; + \propto } \right)$ làm cho dấu của vế trái dương. $ \Rightarrow $ Đáp số chính xác là D
VD2-[Chuyên Thái Bình 2017 ] Giải bất phương trình ${2^{{x^2} – 4}} \ge {5^{x – 2}}$ :
A. $x \in \left( { – \propto ; – 2} \right) \cup \left( {{{\log }_2}5; + \propto } \right)$
B. $x \in \left( { – \propto ; – 2} \right] \cup \left( {{{\log }_2}5; + \propto } \right)$
C. $x \in \left( { – \propto ;{{\log }_2}5 – 2} \right) \cup \left( {2; + \propto } \right)$
D. $x \in \left( { – \propto ;lo{g_2}5 – 2} \right] \cup \left[ {2; + \propto } \right)$
GIẢI
Bất phương trình $ \Leftrightarrow {2^{{x^2} – 4}} – {5^{x – 2}} \ge 0$ .Đăng nhập MODE 7 và nhập vế trái vào máy tính Casio

Quan sát các cận của đáp số là $ – 2;2;{\log _2}5 \approx 2.32;{\log _2}5 – 2 \approx 0.32$ nên ta phải thiết lập miền giá trị của X sao cho X chạy qua các giá trị này . Ta thiết lập Start -3 End 3 Step 1:3
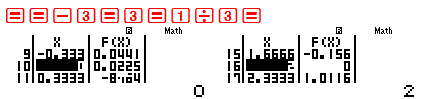
Quan sát bảng giá trị ta thấy rõ ràng hai khoảng $\left( { – \propto ;0.32 = lo{g_2}5} \right)$ và $\left( {2; + \propto } \right)$ làm cho dấu của vế trái dương. $ \Rightarrow $ Đáp số chính xác là C
VD3-[Thi HSG tỉnh Ninh Bình 2017 ]
Tìm tập nghiệm S của bất phương trình ${2.2^x} + {3.3^x} – {6^x} + 1 > 0$ :
A. $S = \left( {2; + \propto } \right)$
B. $S = \left( {0;2} \right)$
C. S=R
D. $\left( { – \propto ;2} \right)$
GIẢI
Đăng nhập MODE 7 và nhập vế trái vào máy tính Casio

Quan sát các cận của đáp số là 0;2 nên ta phải thiết lập miền giá trị của X sao cho X chạy qua các giá trị này . Ta thiết lập Start -4 End 5 Step 1
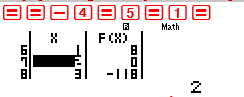
Quan sát bảng giá trị ta thấy rõ ràng hai khoảng $\left( { – \propto ;2} \right)$ làm cho dấu của vế trái dương. $ \Rightarrow $ Đáp số chính xác là C
2) PHƯƠNG PHÁP 4 : LƯỢC ĐỒ CON RẮN
- Bước 1: Chuyển bài toán bất phương trình về bài toán xét dấu bằng cách chuyển hết các số hạng về vế trái. Khi đó bất phương trình sẽ có dạng Vế trái $ \ge 0$ hoặc Vế trái $ \le 0$
- Bước 2: Sử dụng CALC tìm các giá trị tới hạn của (làm cho vế trái = 0 hoặc không xác định ) . Dấu của bất phương trình có trong các khoảng tới hạn là không đổi. Dùng CALC lấy một giá trị đại diện để xét dấu.
Chú ý : Qua 4 phương pháp ta mới thấy trong tự luận thì lược đồ con rắn là lợi hại nhất nhưng trong khi thi trắc nghiệm thì lại tỏ ra yếu thế vì khó dùng và khá dài dòng
Ví dụ minh họa
VD1-[Chuyên Khoa học tự nhiên 2017 ] Bất phương trình ${\log _{\frac{1}{2}}}\left( {{{\log }_3}\frac{{2x + 1}}{{x – 1}}} \right) > 0$ có tập nghiệm là :
A. $\left( { – \propto ; – 2} \right)$
B. $\left( {4; + \propto } \right)$
C. $\left( { – 2;1} \right) \cup \left( {1;4} \right)$
D. $\left( { – \propto ; – 2} \right) \cup \left( {4; + \propto } \right)$
GIẢI
Đề bài xuất hiện các giá trị -2;4;1 ta CALC với các giá tri này để tìm giá trị tới hạn

Lần lượt CALC với cá giá trị -2;4;1
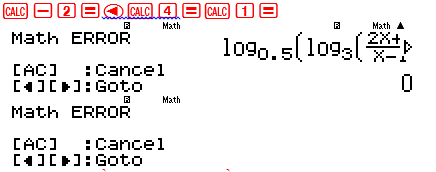
3 giá trị trên đều là giá trị trên đều là giá trị tới hạn nên ta chia thành các khoảng nghiệm $\left( { – \propto ; – 2} \right);\left( { – 2;1} \right);\left( {1;4} \right);\left( {4; + \propto } \right)$
CALC với các giá trị đại diện cho 4 khoảng để lấy dấu là : -3;0;2;5
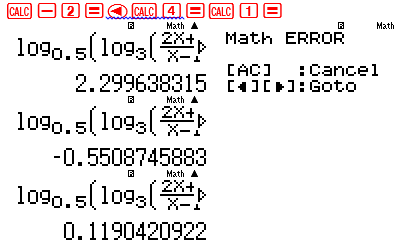
Rõ ràng khoảng nghiệm thứ nhất và thứ tư thỏa mãn $ \Rightarrow $ Đáp số chính xác là D
VD2-[Chuyên Thái Bình 2017 ] Giải bất phương trình ${2^{{x^2} – 4}} \ge {5^{x – 2}}$ :
A. $x \in \left( { – \propto ; – 2} \right) \cup \left( {{{\log }_2}5; + \propto } \right)$
B. $x \in \left( { – \propto ; – 2} \right] \cup \left( {{{\log }_2}5; + \propto } \right)$
C. $x \in \left( { – \propto ;{{\log }_2}5 – 2} \right) \cup \left( {2; + \propto } \right)$
D. $x \in \left( { – \propto ;lo{g_2}5 – 2} \right] \cup \left[ {2; + \propto } \right)$
GIẢI
Đề bài xuất hiện các giá trị $ – 2;lo{g_2}5 – 2;2;{\log _2}5 \approx 2.32$ ta CALC với các giá tri này để tìm giá trị tới hạn
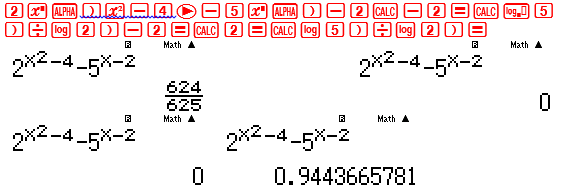
Ta thu được hai giá trị tới hạn ${\log _2}5 – 2$ và 2 $ \Rightarrow $ Đáp số chỉ có thể là C hoặc D
Vì bất phương trình có dấu = nên ta lấy hai cận $ \Rightarrow $ Đáp số chính xác là D
VD3-[Thi HSG tỉnh Ninh Bình 2017 ]
Tìm tập nghiệm S của bất phương trình ${2.2^x} + {3.3^x} – {6^x} + 1 > 0$ :
A. $S = \left( {2; + \propto } \right)$
B. S=(0;2)
C. S= R
D. $\left( { – \propto ;2} \right)$
GIẢI
Đề bài xuất hiện các giá trị 0;2 ta CALC với các giá tri này để tìm giá trị tới hạn
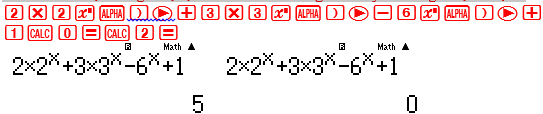
Ta thu được 1 giá trị tới hạn x=2 $ \Rightarrow $ Đáp số đúng là A hoặc D
CALC với các giá trị đại diện cho 2 khoảng để lấy dấu là : 1;3
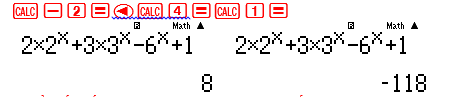
Ta cần lấy dấu dương $ \Rightarrow $ Đáp số chính xác là D
BÀI TẬP TỰ LUYỆN
Bài 1-[Thi thử chuyên Sư phạm Hà Nội lần 1 năm 2017 ]
Bất phương trình $\ln \left[ {\left( {x – 1} \right)\left( {x – 2} \right)\left( {x – 3} \right) + 1} \right] > 0$ có tập nghiệm là :
A. $\left( {1;2} \right) \cup \left( {3; + \propto } \right)$
B. $\left( {1;2} \right) \cap \left( {3; + \propto } \right)$
C. $\left( { – \propto ;1} \right) \cap \left( {2;3} \right)$
D. $\left( { – \propto ;1} \right) \cup \left( {2;3} \right)$
Bài 2-[THPT Lương Thế Vinh – Hà Nội 2017 ] Tập xác định của hàm số $y = \sqrt {{{\log }_{\frac{1}{2}}}\left( {x – 1} \right) – 1} $ là :
A. $\left[ {1; + \propto } \right)$
B. $\left( {1;\frac{3}{2}} \right]$
C. $\left( {1; + \propto } \right)$
D. $\left[ {\frac{3}{2}; + \propto } \right)$
Bài 3-[Chuyên Khoa học tự nhiên 2017 ] Nghiệm của bất phương trình ${\log _{x – 1}}\left( {{x^2} + x – 6} \right) > 1$ là :
A. x> 1
B. $x > \sqrt 5 $
C. $x > 1;x \ne 2$
D. $1 < x < \sqrt 5 ,x \ne 2$
Bài 4-[Chuyên Nguyễn Thị Minh Khai 2017 ] Giải bất phương trình ${\left( {\tan \frac{\pi }{7}} \right)^{{x^2} – x – 9}} \le {\left( {\tan \frac{\pi }{7}} \right)^{x – 1}}$ :
A. $x \le – 2$
B. $x \ge 4$
C. $ – 2 \le x \le 4$
D. $x \le – 2$ hoặc $x \ge 4$
Bài 5-[THPT HN Amsterdam 2017] Bất phương trình ${2^{{x^2}}}{.3^x} < 1$ có bao nhiêu nghiệm nguyên :
A. 1
B. Vô số
C. 0
D. 2
Bài 6-[Thi thử Báo Toán học tuổi trẻ lần 4 năm 2017 ] Tập nghiệm của bất phương trình ${32.4^x} – {18.2^x} + 1 < 0$ là tập con của tập
A. $\left( { – 5; – 2} \right)$
B. $\left( { – 4;0} \right)$
C. $\left( {1;4} \right)$
D. (-3;1)
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Bài 1-[Thi thử chuyên Sư phạm Hà Nội lần 1 năm 2017 ] Bất phương trình $\ln \left[ {\left( {x – 1} \right)\left( {x – 2} \right)\left( {x – 3} \right) + 1} \right] > 0$ có tập nghiệm là :
A. $\left( {1;2} \right) \cup \left( {3; + \propto } \right)$
B. $\left( {1;2} \right) \cap \left( {3; + \propto } \right)$
C. $\left( { – \propto ;1} \right) \cap \left( {2;3} \right)$
D. $\left( { – \propto ;1} \right) \cup \left( {2;3} \right)$
GIẢI
Kiểm tra các giá trị 1;2;3

Cả 3 giá trị trên đều là giá trị tới hạn $ \Rightarrow $ Chia thành 4 khoảng nghiệm $\left( { – \propto ;1} \right);\left( {1;2} \right);\left( {2;3} \right);\left( {3; + \propto } \right)$
CALC với 4 giá trị đại diện cho 4 khoảng này là $0;\frac{3}{2};\frac{5}{2};4$
Ta cần lấy dấu dương $ \Rightarrow $ Lấy khoảng 2 và khoảng 4 $ \Rightarrow $ A là đáp số chính xác
Bài 2-[THPT Lương Thế Vinh – Hà Nội 2017 ] Tập xác định của hàm số $y = \sqrt {{{\log }_{\frac{1}{2}}}\left( {x – 1} \right) – 1} $ là :
A. $\left[ {1; + \propto } \right)$
B. $\left( {1;\frac{3}{2}} \right]$
C. $\left( {1; + \propto } \right)$
D. $\left[ {\frac{3}{2}; + \propto } \right)$
GIẢI
Tập xác định $ \Leftrightarrow {\log _2}\left( {x – 1} \right) – 1 \ge 0$ . Kiểm tra các giá trị $1;\frac{3}{2}$
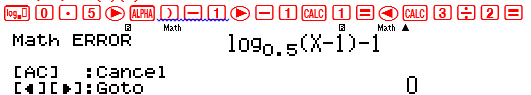
Cả 2 giá trị trên đều là giá trị tới hạn $ \Rightarrow $ Chia thành 3 khoảng nghiệm $\left( { – \propto ;1} \right);\left( {1;\frac{3}{2}} \right);\left( {\frac{3}{2}; + \propto } \right)$
CALC với 3 giá trị đại diện cho 4 khoảng này là $0;1.25;2$

Ta cần lấy dấu dương $ \Rightarrow $ Lấy khoảng 2 $ \Rightarrow $ B là đáp số chính xác
Bài 3-[Chuyên Khoa học tự nhiên 2017 ] Nghiệm của bất phương trình ${\log _{x – 1}}\left( {{x^2} + x – 6} \right) > 1$ là :
A. x>1
B. $x > \sqrt 5 $
C. $x > 1;x \ne 2$
D. $1 < x < \sqrt 5 ,x \ne 2$ GIẢI Bất phương trình $ \Leftrightarrow {\log _{x – 1}}\left( {{x^2} + x – 6} \right) – 1 > 0$ . Quan sát đáp số xuất hiện các giá trị $1;2;\sqrt 5 \approx 2.23$ . Sử dụng MODE 7 với Start 0 End 3 Step 0.25

Rõ ràng $x > \sqrt 5 \approx 2.23$ làm cho vế trái bất phương trình nhận dấu dương $ \Rightarrow $ B là đáp án chính xác
Bài 4-[Chuyên Nguyễn Thị Minh Khai 2017 ] Giải bất phương trình ${\left( {\tan \frac{\pi }{7}} \right)^{{x^2} – x – 9}} \le {\left( {\tan \frac{\pi }{7}} \right)^{x – 1}}$ :
A. $x \le – 2$
B. $x \ge 4$
C. $ – 2 \le x \le 4$
D. $x \le – 2$ hoặc $x \ge 4$
GIẢI
Chuyển bất phương trình về dạng xét dấu ${\left( {\tan \frac{\pi }{7}} \right)^{{x^2} – x – 9}} – {\left( {\tan \frac{\pi }{7}} \right)^{x – 1}} \le 0$
Quan sát đáp số xuất hiện các giá trị -2;4 . Sử dụng MODE 7 với Start -4 End 5 Step 0.5
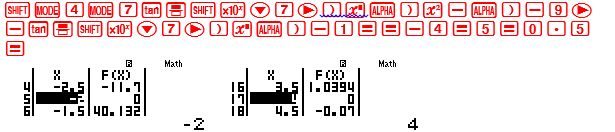
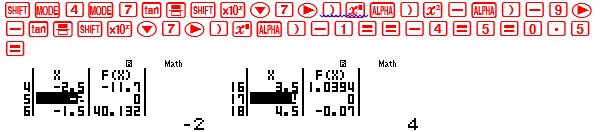
Quan sát bảng giá trị . Rõ ràng $x \le – 2$ và $x \ge 4$ làm cho vế trái bất phương trình $ \ge 0$ $ \Rightarrow $ D là đáp án chính xác
Bài 5-[THPT HN Amsterdam 2017] Bất phương trình ${2^{{x^2}}}{.3^x} < 1$ có bao nhiêu nghiệm nguyên :
A. 1
B. Vô số
C. 0
D. 2
GIẢI
Chuyển bất phương trình về dạng xét dấu ${2^{{x^2}}}{.3^x} – 1 < 0$
Tìm cận thứ nhất bằng chức năng SHIFT SOLVE

Khử cận thứ nhất và tiếp tục dò cận thứ hai
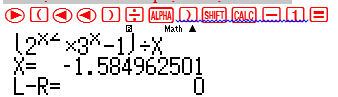
Vậy ta dự đoán khoảng nghiệm là $\left( { – 1.5849…;0} \right)$ . Kiểm tra dấu bằng cách lấy giá trị đại diện x=-1
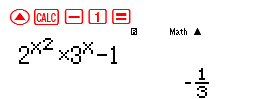
Ta thấy dấu – vậy khoảng nghiệm là $\left( { – 1.5849…;0} \right)$ $ \Rightarrow $ có 1 nghiệm nguyên x=-1
=> Đáp số chính xác là A
Bài 6-[Thi thử Báo Toán học tuổi trẻ lần 4 năm 2017 ] Tập nghiệm của bất phương trình ${32.4^x} – {18.2^x} + 1 < 0$ là tập con của tập
A. (-5;-2)
B. (-4;0)
C. (1;4)
D. (-3;1)
GIẢI
Sử dụng MODE 7 với Start -6 End 6 Step 1

Quan sát bảng giá trị . Rõ ràng khoảng nghiệm làm cho vế trái – thuộc khoảng (-4;0)
$ \Rightarrow $ B là đáp án chính xác.



