1) PHƯƠNG PHÁP
Chứng minh tính đúng sai của mệnh đề mũ – logarit là một dạng tổng hợp khó. Vì vậy để làm được bài này ta phải vận dụng một cách khéo léo các phương pháp mà học từ các bài trước. Luyện tập các ví dụ dưới đây để lấy tích lũy kinh nghiệm xử lý.
2) VÍ DỤ MINH HỌA
VD1-[Đề minh họa THPT Quốc gia 2017] Cho các số thực a,b với $a \ne 1$. Khẳng định nào sau đây là khẳng định đúng ?
A. ${\log _{{a^2}}}\left( {ab} \right) = \frac{1}{2}{\log _a}b$
B. ${\log _{{a^2}}}\left( {ab} \right) = 2 + 2{\log _a}b$
C. ${\log _{{a^2}}}\left( {ab} \right) = \frac{1}{4}{\log _a}b$
D. ${\log _{{a^2}}}\left( {ab} \right) = \frac{1}{2} + \frac{1}{2}{\log _a}b$
GIẢI
Ta hiểu, nếu đáp án A đúng thì phương trình ${\log _{{a^2}}}\left( {ab} \right) – \frac{1}{2}{\log _a}b = 0$ (1) với mọi giá trị của a,b thỏa mãn điều kiện a,b thực và $a \ne 1$ . Ta chọn bất kì A=1.15 và B=0.73 chẳng hạn. Nhập vế trái của (1) vào máy tính Casio rồi dùng lệnh tính giá trị CALC

Máy tính báo kết quả là một số khác 0 vậy vế trái của (1) khác 0 hay đáp án A sai.
Tương tự ta thiết lập phương trình cho đáp án B là ${\log _{{a^2}}}\left( {ab} \right) – 2 – 2{\log _a}b = 0$
Sử dụng chức năng CALC gán giá trị A=1.15 và B=0.73 cho vế trái của (2)

Tiếp tục ra một số khác 0 vậy đáp án B cũng sai
Tiếp tục phép thử này và ta sẽ tìm được đáp án D là đáp án chính xác

Cách tham khảo : Tự luận
Điều kiện $\left\{ \begin{array}{l} a > 0,a \ne 1\\ b > 0,b \ne 1 \end{array} \right.$
Dễ thấy ${\log _{{a^2}}}\left( {ab} \right) = \frac{1}{2}{\log _a}ab = \frac{1}{2}\left( {{{\log }_a}a + {{\log }_a}b} \right) = \frac{1}{2} + \frac{1}{2}{\log _a}b$
Bình luận :
- Chúng ta chú ý phân biệt 2 công thức ${\log _a}{x^m} = m{\log _a}\left| x \right|$ và ${\log _{{a^n}}}x = \frac{1}{n}{\log _{\left| a \right|}}x$
- Theo kinh nghiệm làm nhiều trắc nghiệm của tác giả thì đáp án đúng thường có xu hướng xếp ở đáp án C và D nên ta nên thử ngược từ đáp án D trở xuống thì nhanh tìm được đáp án đúng nhanh hơn.
VD2-[Đề minh họa THPT Quốc gia 2017] Cho 2 số thực a,b với 1<a
A. ${\log _a}b < 1 < {\log _b}a$
B. $1 < {\log _a}b < {\log _b}a$
C. ${\log _b}a < {\log _a}b < 1$
D. ${\log _b}a < 1 < {\log _a}b$
GIẢI
Chọn giá trị a,b thỏa mãn điều kiện a,b thực và 1< a < b. Ta chọn a=1.15 và b=2.05
Tính giá trị số hạng ${\log _a}b$

Tính giá trị của số hạng ${\log _b}a$
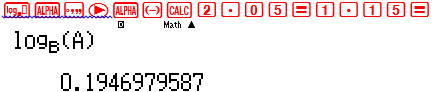
Rõ ràng ${\log _b}a < 1 < {\log _a}b$ $ \Rightarrow $ Đáp số chính xác là D
Cách tham khảo : Tự luận Vì cơ số $a > 1 \Rightarrow {\log _a}a < {\log _a}b \Leftrightarrow 1 < {\log _a}b$ (1) Vì cơ số b>0 $ \Rightarrow {\log _b}a < {\log _b}b \Leftrightarrow {\log _b}a < 1$ (2)
Kết hợp (1) và (2) ta có : ${\log _b}a < 1 < {\log _a}b$ $ \Rightarrow $ D là đáp án chính xác
Bình luận : • Chú ý tính chất của cơ số : Nếu a>1 thì ${\log _a}u > {\log _a}v \Leftrightarrow u > v$ nhưng nếu 0<a<1 thì ${\log _a}u > {\log _a}v \Leftrightarrow u < v$
VD5-[THPT Bảo Lâm – Lâm Đồng 2017] Cho hệ thức ${a^2} + {b^2} = 7ab\,\,\,\left( {a,b > 0} \right)$. Khẳng định nào sau đây đúng ?
A. $4{\log _2}\frac{{a + b}}{6} = {\log _2}a + {\log _2}b$
B. $2{\log _2}\left( {a + b} \right) = {\log _2}a + {\log _2}b$
C. ${\log _2}\frac{{a + b}}{3} = 2\left( {{{\log }_2}a + {{\log }_2}b} \right)$
D. $2{\log _2}\frac{{a + b}}{3} = {\log _2}a + {\log _2}b$
GIẢI
Vì a,b>0 nên ta chọn a=1, khi đó b sẽ thỏa mãn hệ thức $1 + {b^2} = 7b \Leftrightarrow {b^2} – 7b + 1 = 0 \Leftrightarrow b = \frac{{7 \pm 3\sqrt 5 }}{2}$. Chọn $b = \frac{{7 + 3\sqrt 5 }}{2}$
Lưu a=1 vào biến A
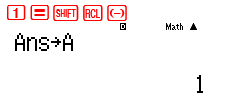
Lưu $b = \frac{{7 + 3\sqrt 5 }}{2}$ vào biến B

Nếu đáp án A đúng thì $4{\log _2}\frac{{a + b}}{6} – {\log _2}a – {\log _2}b = 0$ Để kiểm tra sự đúng sai của hệ thức này ta nhập vế trái vào máy tính Casio rồi nhấn nút =nếu kết quả ra 0 là đúng còn khác 0 là sai

Kết quả biểu thức vế trái ra khác 0 vậy đáp án A sai
Tương tự như vậy với các đáp án B, C, D và cuối cùng ta tìm được đáp án D là đáp án chính xác

Cách tham khảo : Tự luận
Biến đổi ${a^2} + {b^2} = 7ab\, \Leftrightarrow {\left( {a + b} \right)^2} = 9ab \Leftrightarrow {\left( {\frac{{a + b}}{9}} \right)^2} = ab$
Logarit cơ số 2 cả 2 vế ta được : ${\log _2}{\left( {\frac{{a + b}}{3}} \right)^2} = {\log _2}ab$ $ \Leftrightarrow 2{\log _2}\frac{{a + b}}{3} = {\log _2}a + {\log _2}b$
Bình luận: Một bài toán biến đổi tương đối là zic zắc đòi hỏi học sinh phải nhuần nhuyễn các công thức và ác phép biến đổi Logarit
VD4-[Chuyên Vị Thanh – Hậu Giang 2017] Nếu ${\log _7}x = 8{\log _7}a{b^2} – 2{\log _7}{a^3}b,\,\left( {a,b > 0} \right)$ thì x bằng :
A. ${a^4}{b^6}$
B. ${a^2}{b^{14}}$
C. ${a^6}{b^{12}}$
D. ${a^8}{b^{14}}$
GIẢI
Chọn giá trị a,b thỏa mãn điều kiện a,b>0 thực. Ta tiếp tục chọn a=1.15 và b=2.05
Ta có ${\log _7}x = 8{\log _7}a{b^2} – 2{\log _7}{a^3}b \Leftrightarrow x = {7^{8{{\log }_7}a{b^2} – 2{{\log }_7}{a^3}b}}$

Vậy ta biết được x=30616.09068
Tới đây ta chỉ cần tính giá trị các đáp án A, B, C, D xem đáp án nào bằng 30616.09068 là xong
Và ta thấy đáp số B là đáp số chính xác

Cách tham khảo : Tự luận
Thu gọn ${\log _7}x = {\log _7}{\left( {a{b^2}} \right)^8} – {\log _7}{\left( {{a^3}b} \right)^2} = {\log _7}\left( {{a^8}{b^{16}}} \right) – {\log _7}{a^6}{b^2} = {\log _7}\frac{{{a^8}{b^{16}}}}{{{a^6}{b^2}}} = {\log _7}{a^2}{b^{14}}$
Vì cơ số b>1 $ \Rightarrow {\log _b}a < {\log _b}b \Leftrightarrow {\log _b}a < 1$ (2)
Kết hợp (1) và (2) ta có : ${\log _b}a < 1 < {\log _a}b$ $ \Rightarrow $ D là đáp án chính xác Bình luận : • Chú ý tính chất của cơ số : Nếu a>1 thì ${\log _a}u > {\log _a}v \Leftrightarrow u > v$ nhưng nếu 0<a<1 thì ${\log _a}u > {\log _a}v \Leftrightarrow u < v$
VD5-[THPT Bảo Lâm – Lâm Đồng 2017] Cho hàm số $f\left( x \right) = {3^{{x^2}}}{.4^x}$. Khẳng định nào sau đây sai
A. $f\left( x \right) > 9 \Leftrightarrow {x^2} + 2x{\log _3}2 > 2$
B. $f\left( x \right) > 9 \Leftrightarrow {x^2}{\log _2}3 + 2x > 2{\log _2}3$
C. $f\left( x \right) > 9 \Leftrightarrow 2x\log 3 + x\log 4 > \log 9$
D. $f\left( x \right) > 9 \Leftrightarrow {x^2}\ln 3 + x\ln 4 > 2\ln 3$
GIẢI
Từ điều kiện đề bài, ta khai thác để tìm x : $f\left( c \right) > 9 \Leftrightarrow {3^{{x^2}}}{.4^x} – 9 > 0$ (1)
Dùng Mode 7 để dò khoảng nghiệm của (1)
![]()
Quan sát bảng giá trị (chú ý lấy phần F(X)>0)

Thấy x< -2, … Ta đặt x<a
Thấy x< 0, … Ta đặt x>b
Để phóng to khoảng nghiệm và tìm chính xác a,b hơn ta chọn lại miền giá trị của X

Vậy x>0.75 và x< -2.25
Việc cuối cùng là ta chỉ cần dò khoảng nghiệm xuất hiện ở đáp án A, B, C, D xem khoảng nào trùng với khoảng nghiệm trên thì là đúng.

Ta thấy đáp án A trùng khoảng nghiệm vậy đáp án A là đáp án chính xác
Cách tham khảo : Tự luận
Biến đổi $f\left( c \right) > 9 \Leftrightarrow {3^{{x^2}}}{.4^x} > 9 \Leftrightarrow \frac{{{3^{{x^2}}}}}{9} > \frac{1}{{{4^x}}} \Leftrightarrow {3^{{x^2} – 2}} > {4^{ – x}}$
Logarit cơ số 3 cả 2 vế ta được : ${\log _3}\left( {{3^{{x^2} – 2}}} \right) > {\log _3}\left( {{4^{ – x}}} \right) \Leftrightarrow {x^2} – 2 > – x{\log _3}4 \Leftrightarrow {x^2} + 2x{\log _3}4 > 2$
Bình luận :
• Một bài tự luận ta nhìn là biết dùng phương pháp logarit cả 2 vế luôn vì 2 số hạng trong bất phương trình khác cơ số và số mũ có nhân tử chung x
BÀI TẬP TỰ LUYỆN
Bài 1-[HSG tỉnh Ninh Bình 2017] Cho các số dương a,b,c và $a \ne 1$. Khẳng định nào đúng ?
A. ${\log _a}b + {\log _a}c = \log \left( {b + c} \right)$
B. ${\log _a}b + {\log _a}c = {\log _a}\left| {b – c} \right|$
C. ${\log _a}b + {\log _a}c = {\log _a}\left( {bc} \right)$
D. ${\log _a}b + {\log _a}c = {\log _a}\left( {\frac{b}{c}} \right)$
Bài 2-[Thi thử tính Lâm Đồng – Hà Nội 2017] Cho 2 số thực dương a,b với $a \ne 1$. Khẳng định nào sau đây là khẳng định đúng ?
A. ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) = \frac{1}{3}\left( {1 + \frac{1}{2}{{\log }_a}b} \right)$
B. ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) = \frac{1}{3}\left( {1 – 2{{\log }_a}b} \right)$ C. ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) = \frac{1}{3}\left( {1 – \frac{1}{2}{{\log }_a}b} \right)$
D. ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) = 3\left( {1 – \frac{1}{2}{{\log }_a}b} \right)$
Bài 3-[Chuyên Nguyễn Thị Minh Khai 2017] Nếu ${a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}$ và ${\log _b}\frac{1}{2} < {\log _b}\frac{2}{3}$ thì ta có :
A. 0< a < b< 1
B. 0< b < a < 1
C. 0 < a < 1 < b
D. 1< a < b
Bài 4-[THPT Lương Thế Vinh – HN 2017] Khẳng định nào sau đây là đúng ?
A.Hàm số $y = {e^{1999x}}$ nghịch biến trên R
B. Hàm số y=lnx đồng biến trên $\left( {0; + \propto } \right)$
C. ${\log _3}\left( {a + b} \right) = {\log _3}a + {\log _3}b$
D. ${\log _a}b.{\log _b}c.{\log _c}a = 1$ với mọi $a,b,c \in R$
Bài 5-[Chuyên Vị Thanh – Hậu Giang 2017] Cho 0<a<1. Tìm mệnh đề sai trong các mệnh đề sau : A. ${\log _a}x > 0$thì 0<x<1
B. ${\log _a}x < 0$ thì x>1
C. \[{x_1} < {x_2}\] thì ${\log _a}{x_1} < {\log _a}{x_2}$
D. Đồ thị hàm số $y = {\log _a}x$ có tiệm cận đứng là trục tung
Bài 6-[THPT Lương Thế Vinh – HN 2017] Tìm mệnh đề đúng trong các mệnh đề sau ?
A. Hàm số $y = {\log _a}x$ với 0<a<1 là một hàm số đồng biến trên khoảng $\left( {0; + \propto } \right)$ B. Hàm số $y = {\log _a}x$ với a>1 là một hàm số nghịch biến trên khoảng $\left( {0; + \propto } \right)$
C. Hàm số $y = {\log _a}x$ $\left( {0 < a;a \ne 1} \right)$ có tập xác định R
D. Đồ thị các hàm số $y = {\log _a}x$ và $y = {\log _{\frac{1}{a}}}x\,\,\,\left( {0 < a;a \ne 1} \right)$ đối xứng nhau qua trục hoành
Bài 7-[THPT HN-Amsterdam 2017] Cho a,b là các số thực dương và $a \ne 1$. Khẳng định nào sau đây đúng ?
A. ${\log _{\sqrt a }}\left( {{a^2} + ab} \right) = 2 + 2{\log _a}\left( {a + b} \right)$
B. ${\log _{\sqrt a }}\left( {{a^2} + ab} \right) = 4{\log _a}(a + b)$
C. ${\log _{\sqrt a }}\left( {{a^2} + ab} \right) = 1 + 4{\log _a}b$
D. ${\log _{\sqrt a }}\left( {{a^2} + ab} \right) = 4 + 2{\log _a}b$
Bài 8-[THPT Kim Liên – HN 2017] Trong các khẳng định sau, khẳng định nào sai :
A. Hàm số y=logx là hàm số logarit
B. Hàm số $y = {\left( {{3^{ – 1}}} \right)^x}$ là hàm số mũ
C. Hàm số $y = {\left( \pi \right)^x}$ nghịch biến trên R
D. Hàm số y=lnx đồng biến trên khoảng $\left( {0; + \propto } \right)$
Bài 9-[Sở GD-ĐT Nam Định 2017] Cho $a > 0;a \ne 1$ và x,y là 2 số dương. Khẳng định nào sau đây là khẳng định đúng ?
A. ${\log _a}\frac{x}{y} = \frac{{{{\log }_a}x}}{{{{\log }_a}y}}$
B. ${\log _a}\left( {x – y} \right) = \frac{{{{\log }_a}x}}{{{{\log }_a}y}}$
C. ${\log _a}\frac{x}{y} = {\log _a}x – {\log _a}y$
D. ${\log _a}\left( {x – y} \right) = {\log _a}x – {\log _a}y$
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Bài 1-[HSG tỉnh Ninh Bình 2017] Cho các số dương a,b,c và $a \ne 1$. Khẳng định nào đúng ?
A. ${\log _a}b + {\log _a}c = \log \left( {b + c} \right)$
B. ${\log _a}b + {\log _a}c = {\log _a}\left| {b – c} \right|$
C. ${\log _a}b + {\log _a}c = {\log _a}\left( {bc} \right)$
D. ${\log _a}b + {\log _a}c = {\log _a}\left( {\frac{b}{c}} \right)$
GIẢI
Chọn a=1.25, b=1.125, c=2.175 rồi lưu các giá trị này vào A, B, C

Kiểm tra 4 đáp án và ta có đáp án C chính xác vì ${\log _a}b + {\log _a}c – {\log _a}\left( {bc} \right) = 0$

Bài 2-[Thi thử tính Lâm Đồng – Hà Nội 2017] Cho 2 số thực dương a,b với $a \ne 1$. Khẳng định nào sau đây là khẳng định đúng ?
A. ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) = \frac{1}{3}\left( {1 + \frac{1}{2}{{\log }_a}b} \right)$
B. ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) = \frac{1}{3}\left( {1 – 2{{\log }_a}b} \right)$
C. ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) = \frac{1}{3}\left( {1 – \frac{1}{2}{{\log }_a}b} \right)$
D. ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) = 3\left( {1 – \frac{1}{2}{{\log }_a}b} \right)$
GIẢI
Chọn a=1.25, b=1.125 rồi lưu các giá trị này vào A, B

Kiểm tra 4 đáp án và ta có đáp án C chính xác vì ${\log _{{a^3}}}\left( {\frac{a}{{\sqrt b }}} \right) – \frac{1}{3}\left( {1 – \frac{1}{2}{{\log }_a}b} \right) = 0$

Bài 3-[Chuyên Nguyễn Thị Minh Khai 2017] Nếu ${a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}$ và ${\log _b}\frac{1}{2} < {\log _b}\frac{2}{3}$ thì ta có:
A. 0< a < b< 1
B. 0< b < a < 1
C. 0 < a < 1 < b
D. 1< a < b
GIẢI
Từ ${a^{\frac{3}{4}}} > {a^{\frac{4}{5}}} \Leftrightarrow {a^{\frac{3}{4}}} – {a^{\frac{4}{5}}} > 0$ . Tìm miền giá trị của a bằng chức năng MODE 7$ \Rightarrow 0 < a < 1$

Từ ${\log _b}\frac{1}{2} < {\log _b}\frac{2}{3} \Leftrightarrow {\log _b}\frac{1}{2} – {\log _b}\frac{2}{3} < 0$ . Tìm miền giá trị của b bằng chức năng MODE 7$ \Rightarrow b > 1$

Tóm lại 0<a<1
Bài 4-[THPT Lương Thế Vinh – HN 2017] Khẳng định nào sau đây là đúng ?
A.Hàm số $y = {e^{1999x}}$ nghịch biến trên R
B. Hàm số y=lnx đồng biến trên $\left( {0; + \propto } \right)$
C. ${\log _3}\left( {a + b} \right) = {\log _3}a + {\log _3}b$
D. ${\log _a}b.{\log _b}c.{\log _c}a = 1$ với mọi $a,b,c \in R$
GIẢI
Khẳng định A có số mũ quá cao nên ta để lại sau cùng.
Kiểm tra khẳng định B bằng chức năng MODE 7. Ta thấy F(X) luôn tăng $ \Rightarrow $ B chính xác

Vì sao đáp án C, D sai thì ta chỉ việc chọn a=1.25, b=-3.75 là rõ luôn (vì điều kiện ràng buộc không có nên để đảm bảo tính tổng quát ta sẽ chọn một giá trị dương một giá trị âm)
Bài 5-[Chuyên Vị Thanh – Hậu Giang 2017] Cho 0<a<1. Tìm mệnh đề sai trong các mệnh đề sau
A. ${\log _a}x > 0$thì 0<x<1
B. ${\log _a}x < 0$ thì x>1
C. \[{x_1} < {x_2}\] thì ${\log _a}{x_1} < {\log _a}{x_2}$
D. Đồ thị hàm số $y = {\log _a}x$ có tiệm cận đứng là trục tung
GIẢI
Cho 0<a<1 vậy ta chọn a=0.123. Kiểm tra đáp số A ta dò miền nghiệm của phương trình ${\log _a}x > 0$ xem miền nghiệm có trùng với 0<x<1 không là xong. Để làm việc này ta sử dụng chức năng MODE 7


Quan sát bảng giá trị ta được miền nghiệm 0<x<1 (phần làm cho F(X)>0) , miền nghiệm này giống miền 0<x<1 vậy đáp số A đúng
Tương tự cách kiểm tra đáp án A ta áp dụng cho đáp án B thì thấy B đúng
Để kiểm tra đáp án C ta chọn hai giá trị ${x_1} = 2 < {x_2} = 5$ . Thiết lập hiệu ${\log _a}{x_1} – {\log _a}{x_2}$. Nếu hiệu này ra âm thì C đúng còn ra dương thì C sai. Để tính hiệu này ta sử dụng chức năng CALC

Vậy hiệu ${\log _a}{x_1} – {\log _a}{x_2}$ lớn hơn 0 hay ${\log _a}{x_1} > {\log _a}{x_2}$. Vậy đáp án C là sai
Bài 6-[THPT Lương Thế Vinh – HN 2017] Tìm mệnh đề đúng trong các mệnh đề sau ?
A. Hàm số $y = {\log _a}x$ với 0<a<1 là một hàm số đồng biến trên khoảng $\left( {0; + \propto } \right)$
B. Hàm số $y = {\log _a}x$ với a>1 là một hàm số nghịch biến trên khoảng $\left( {0; + \propto } \right)$
C. Hàm số $y = {\log _a}x$ $\left( {0 < a;a \ne 1} \right)$ có tập xác định R
D. Đồ thị các hàm số $y = {\log _a}x$ và $y = {\log _{\frac{1}{a}}}x\,\,\,\left( {0 < a;a \ne 1} \right)$ đối xứng nhau qua trục hoành
GIẢI
Câu D khó hiểu nhất nên ta ưu tiên đi xác định đúng sai các đáp án A , B , C trước
Kiểm tra khẳng định đáp án A bằng chức năng MODE 7 với a=0.5 thỏa 9<a<1 . Ta thấy F(X) giảm
$ \Rightarrow $ A sai $ \Rightarrow $ Đáp án B cũng sai

Kiểm tra khẳng định đáp án C bằng chức năng MODE 7. Ta thấy hàm số không xác định khi $x \le 0$
$ \Rightarrow $ Đáp án C cũng sai $ \Rightarrow $ Tóm lại đáp án chính xác là D

Nếu tím hiểu vì sao hai đồ thị trên đối xứng nhau qua trục hoành thì ta phải hiểu ý nghĩa “nếu đồ thị hàm số y=f(x) và đồ thị hàm số y=g(x) đối xứng nhau qua trục hoành thì f(x)=-g(x)”
Vậy ta sẽ chọn a=2, x=5 rồi tính $y = {\log _2}5 = 2.32…$ và $y = {\log _{\frac{1}{2}}}x = – 2.32…$ $ \Rightarrow $ D đúng



