Link pdf tải đề và hướng dẫn chi tiết: Tại đây
Câu 1: Một du khách vào chuồng đua ngựa đặt cược, lần đầu tiên đặt 20000 đồng, mỗi lần sau tiền đặt gấp đôi lần tiền đặt cược trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khách đó thắng hay thua bao nhiêu ?
A. Thắng 20000 đồng B. Hòa vốn.
C. Thua 20000 đồng. D. Thua 40000 đồng.
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
B. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn chứa một đường thẳng cố định.
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
Câu 26: Cho hàm số $y = {x^{ – \sqrt {2018} }}$. Mệnh đề nào dưới đây là đúng về đường tiệm cận của đồ thị hàm số ?
A. Không có tiệm cận.
B. Có một tiệm cận ngang và không có tiệm cận đứng.
C. Có một tiệm cận ngang và một tiệm cận đứng.
D. Không có tiệm cận ngang và có một tiệm cận đứng.
Câu 30: Một kim tự tháp ở Ai Cập được xây dựng vào khoảng 2500 trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao \(150m\), cạnh đáy dài \(220m\). Diện tích xung quanh của kim tự tháp này là ?
A. \(1100\sqrt {346} ({m^2})\)
B. \(4400\sqrt {346} ({m^2})\)
C. \(2200\sqrt {346} ({m^2})\)
D. \(2420000({m^3})\)
Câu 37: Cho hàm số\(y = {x^4} – 4{x^2} + m{\rm{ }}\left( {{C_m}} \right)\). Giả sử \(({C_m})\) cắt trục hoành tại \(4\) điểm phân biệt sao cho hình phẳng giới hạn bởi \(({C_m})\) với trục hoành có diện tích phần phía trên trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó m thuộc khoảng nào dưới đây ?
A. \(m \in \left( { – 1;1} \right)\)
B. \(m \in \left( {3;5} \right)\)
C. \(m \in \left( {2;3} \right)\)
D. \(m \in \left( {5; + \infty } \right)\)
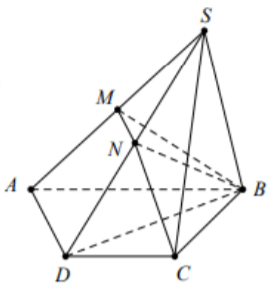
Câu 42: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành có thể tích bằng \(V\). Gọi \(E\) là điểm trên cạnh \(SC\) sao cho \(EC = 2ES\). Gọi \(\left( \alpha \right)\) là mặt phẳng chứa \(AE\) và song song với \(BD\), \(\left( \alpha \right)\) cắt \(SB,SD\) lần lượt tại hai điểm \(M,N\). Tính theo \(V\) thể tích khối chóp \(S.AMEN\).
A. \(\frac{{3V}}{8}\)
B. \(\frac{{3V}}{{16}}\)
C. \(\frac{V}{9}\).
D. \(\frac{V}{6}\).
Câu 45: Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(a\). Hình chiếu vuông góc của đỉnh \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là điểm \(H\) trên cạnh \(AB\) sao cho \(HA = 2HB\). Góc giữa \(SC\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^0}\). Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) theo \(a\).
A. \(\frac{{a\sqrt {42} }}{3}\).
B. \(\frac{{a\sqrt 6 }}{7}\).
C. \(\frac{{a\sqrt {42} }}{8}\).
D. \(\frac{{a\sqrt 6 }}{8}\).
Câu 50: Có 4 cặp vợ chồng được xếp ngồi trên một chiếc ghế dài có 8 chỗ. Biết rằng mỗi người vợ chỉ ngồi cạnh chồng của mình hoặc ngồi cạnh một người phụ nữ khác. Hỏi có bao nhiêu cách sắp xếp chỗ ngồi thỏa mãn.
A. 816
B. 18
C. 8!
D. 604