1. Nguyên hàm là gì?
Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
2. Tính chất nguyên hàm
Nguyên hàm có 3 tính chất quan trọng cần nhớ:
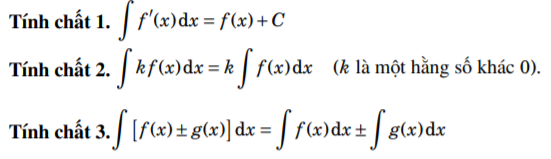
2. Bảng nguyên hàm
a) Bảng công thức nguyên hàm cơ bản

b) Bảng nguyên hàm mở rộng

3. Các phương pháp tính nguyên hàm
Dạng 1. Nguyên hàm cơ bản
Dạng 2. Sử dụng phương pháp ĐỔI BIẾN để tìm nguyên hàm
a) Đổi biến tổng quát
- Bước 1: Chọn t = φ(x). Trong đó φ(x) là hàm số mà ta chọn thích hợp.
- Bước 2: Tính vi phân hai về dt = φ'(x)dx
- Bước 3: Biểu thị f(x)dx = g[φ(x)]φ'(x)dx = g(t)dt.
- Bước 4: Khi đó $I = \int {f\left( x \right)dx} $ $ = \int {g\left( t \right)dt} $ $ = G\left( t \right) + C$
Ví dụ: Tìm nguyên hàm của hàm số $I = \int {\frac{1}{{x\sqrt {\ln x + 1} }}dx} $
Hướng dẫn giải
- Bước 1: Chọn $t = \sqrt {\ln x + 1} \Rightarrow {t^2} = \ln x + 1$
- Bước 2: Tính vi phân hai về dt = – 3sinx.dx
- Bước 3: Biểu thị $\int {f\left( x \right)dx} = – \frac{1}{3}\int {\frac{1}{t}.dt} $
- Bước 4: Khi đó $I = – \frac{1}{3}\ln \left| t \right| + C$ $ = – \frac{1}{3}\ln \left| {1 + 3\cos x} \right| + C$
b) Đổi biến dạng 1

c) Đổi biến dạng 2

Dạng 3. Nguyên hàm từng phần

Nguyên tắc chung để đặt u và dv: Tìm được v dễ dàng và ∫v.du tính được
Nhấn mạnh: Thứ tự ưu tiên khi chọn đặt u: “Nhất lô, nhì đa, tam lượng, tứ mũ” (hàm lôgarit, hàm đa thức, hàm lượng giác, hàm mũ).
Ví dụ: Tìm nguyên hàm của hàm số f(x) = x.e2x
Hướng dẫn giải
Bước 1: Đặt $\left\{ \begin{array}{l} u = \ln \left( {2x} \right)\\ dv = x.dx \end{array} \right. \Rightarrow \left\{ \begin{array}{l} du = \frac{1}{x}\\ v = \frac{{{x^2}}}{2} \end{array} \right.$
Bước 2: Ta thấy $F\left( x \right) = \int {f\left( x \right)} dx$ $ = \frac{{{x^2}}}{2}.\ln \left( {2x} \right) – \int {\frac{1}{x}.\frac{{{x^2}}}{2}} dx$ $ = \frac{{{x^2}}}{2}.\ln \left( {2x} \right) – \frac{{{x^2}}}{4} + C$ $ = \frac{{{x^2}}}{2}.\left( {\ln \left( {2x} \right) – \frac{1}{2}} \right) + C$
Dạng 4. cách tính nguyên hàm bằng máy tính
Cho nguyên hàm $\int {f\left( x \right)dx} $ = F(x) + C. Hãy tìm f(x) hoặc F(x)
Hướng dẫn
Để giải, mình sẽ hướng dẫn cách bấm máy tính nguyên hàm nhanh theo 3 bước sau:
Bước 1: Nhấn shift $\frac{d}{{dx}}\left( {F\left( x \right)} \right){|_{x = X}} – f\left( X \right)$
Bước 2: Nhấn phím Calc nhập X = 2.5
Bước 3: Đánh giá nghiệm
- Nếu kết quả bằng 0 (gần bằng 0 ) thì đó là đáp án cần chọn
Ví dụ: Tìm tất cả nghiệm của hàm số f(x) = $\frac{1}{{2x + 3}}$ là
A. $\frac{1}{2}.ln\left| {2x + 3} \right| + C$
B. $\frac{1}{2}.ln\left( {2x + 3} \right) + C$
C. ln|2x + 3| + C
D. $\frac{1}{{\ln 2}}.$ln|2x + 3| + C
Hướng dẫn bấm máy tính
Bước 1: Nhập vào máy tính casio $\frac{d}{{dx}}\left( {\frac{1}{2}.\ln \left( {\left| {2x + 3} \right|} \right)} \right){|_{x = X}} – \frac{1}{{2x + 3}}$
Bước 2: CALC X = -2
Lưu ý: Trong kết quả A và C nếu cho X = 2 thì đều cho kết quả là 0. Vậy khi có trị tuyệt đối thì cho X một giá trị cho biểu thức trong trị tuyệt đối âm.
Kết luận: Chọn đáp án A.
Dạng 5. Tính nguyên hàm của hàm số
Tìm nguyên hàm dạng $\left[ \begin{array}{l} I = \int {P(x)\sin axdx} \\ I = \int {P(x)c{\rm{osaxdx}}} \end{array} \right.$ với $P(x)$ là một đa thức
Ta lựa chọn một trong hai cách sau:
Cách 1: Sử dụng nguyên hàm từng phần, thực hiện theo các bước sau:
- Bước 1: Đặt: $\left\{ \begin{array}{l} u = P(x)\\ dv = \left[ \begin{array}{l} {\mathop{\rm s}\nolimits} {\rm{inaxdx}}\\ {\rm{cosaxdx}} \end{array} \right. \end{array} \right.$ $ \to \left\{ \begin{array}{l} du = P'(x)dx\\ v = \left[ \begin{array}{l} \frac{{ – 1}}{a}c{\rm{osax}}\\ \frac{{\rm{1}}}{{\rm{a}}}\sin ax \end{array} \right. \end{array} \right.$
- Bước 2: Thay vào công thức nguyên hàm từng phần.
- Bước 3: Tiếp tục thủ tục như trên ta sẽ khử được bậc của đa thức.
* Cách 2: Sử dụng phương pháp hệ số bất định, thực hiện theo các bước sau:
- Bước 1: Ta có: $I = \int {P(x)c{\rm{osaxdx}}} $ ${{\rm{ = A(x)sinax + B(x)cosax + C}}}$ $(1)$, trong đó $A(x)$ và $B(x)$ là các đa thức cùng bậc với $P(x).$
- Bước 2: Lấy đạo hàm hai vế của $(1)$: $P(x)c{\rm{osax}}$ ${\rm{ = A'(x)cosax – A(x)a}}{\rm{.sinax}}$ ${\rm{ + B'(x)sinax + aB(x)cosax}}.$
- Bước 3: Sử dụng phương pháp hệ số bất định ta xác định được $A(x)$ và $B(x).$
Nhận xét: Nếu bậc của đa thức lớn hơn $3$ thì cách 1 tỏ ra cồng kềnh, vì khi đó ta thực hiện số lần nguyên hàm từng phần bằng với số bậc của đa thức, cho nên ta đi đến nhận định như sau:
- Nếu bậc của đa thức nhỏ hơn hoặc bằng $2$: Ta sử dụng cách 1.
- Nếu bậc của đa thức lớn hơn hoặc bằng $3$: Ta sử dụng cách 2.
Ví dụ: Tìm nguyên hàm $\int {x{{\sin }^2}xdx} .$
Giải
Ta có: $I = \int {x\left( {\frac{{1 – c{\rm{os2x}}}}{2}} \right)dx} $ ${ = \frac{1}{2}\int {xdx} – \frac{1}{2}\int {x\cos 2xdx} }$ ${ = \frac{1}{4}{x^2} – \frac{1}{2}J}$ $(1).$
Tính: $J = \int {x\cos 2xdx} .$
Đặt: $\left\{ \begin{array}{l} u = x\\ dv = c{\rm{os2xdx}} \end{array} \right.$ $ \to \left\{ \begin{array}{l} du = dx\\ v = \frac{1}{2}\sin 2x \end{array} \right.$ $ \Rightarrow J = \frac{x}{2}\sin 2x – \frac{1}{2}\int {\sin 2xdx} $ ${ = \frac{x}{2}\sin 2x + \frac{1}{4}c{\rm{os2x + C}}}.$
Thay vào $(1)$: $I = \frac{1}{4}{x^2} – \frac{1}{2}\left( {\frac{x}{2}\sin 2x + \frac{1}{4}c{\rm{os2x}}} \right)$ $ = \frac{1}{4}\left( {{x^2} – x\sin 2x – \frac{1}{2}c{\rm{os2x}}} \right) + C.$
3. Bài tập nguyên hàm
Bài tập 2: Tìm nguyên hàm $I = \int {\left( {{x^3} – {x^2} + 2x – 3} \right){\mathop{\rm s}\nolimits} {\rm{inx}}dx} .$
Giải
Theo nhận xét trên, ta sử dụng phương pháp hệ số bất định. Ta có: $I = \int {\left( {{x^3} – {x^2} + 2x – 3} \right){\mathop{\rm s}\nolimits} {\rm{inx}}dx} $ $ = \left( {{a_1}{x^3} + {b_1}{x^2} + {c_1}x + {d_1}} \right)c{\rm{osx}}$ ${\rm{ + }}\left( {{a_2}{x^3} + {b_2}{x^2} + {c_2}x + {d_2}} \right){\mathop{\rm s}\nolimits} {\rm{inx}}$ $(1).$
Lấy đạo hàm hai vế của $(1)$:
$ \Leftrightarrow \left( {{x^3} – {x^2} + 2x – 3} \right){\mathop{\rm s}\nolimits} {\rm{inx}}$ ${\rm{ = [}}{{\rm{a}}_{\rm{2}}}{x^3} + \left( {3{a_1} + {b_2}} \right){x^2}$ $ + \left( {2{b_1} + {c_2}} \right)x + {c_1} + {d_2}{\rm{]cosx}}$
$ – [{{\rm{a}}_{\rm{1}}}{x^3} – \left( {3{a_2} – {b_1}} \right){x^2}$ $ – \left( {2{b_2} – {c_1}} \right)x + {c_2} – {d_1}]\sin x$ $(2).$
Đồng nhất thức ta được: $\left\{ \begin{array}{l} {a_2} = 0\\ 3{a_1} + {b_2} = 0\\ 2{b_1} + {c_2} = 0\\ {c_1} + {d_2} = 0 \end{array} \right.$ và $\left\{ \begin{array}{l} – {a_1} = 1\\ 3{a_2} – {b_1} = – 1\\ 2{b_2} – {c_1} = 2\\ – {c_2} + {d_1} = – 3 \end{array} \right.$ $ \Rightarrow \left\{ \begin{array}{l} {a_1} = – 1;{a_2} = 0\\ {b_1} = 1;{b_2} = 3\\ {c_1} = 4;{c_2} = – 2\\ {d_1} = 1;{d_2} = – 4 \end{array} \right.$
Khi đó: $I = \left( { – {x^3} + {x^2} + 4x + 1} \right)c{\rm{osx}}$ ${\rm{ + }}\left( {{\rm{3}}{{\rm{x}}^{\rm{2}}} – 2x + 4} \right){\mathop{\rm s}\nolimits} {\rm{inx + C}}.$